Closed-form Two-way TOA Localization and Synchronization for User Devices with Motion and Clock Drift

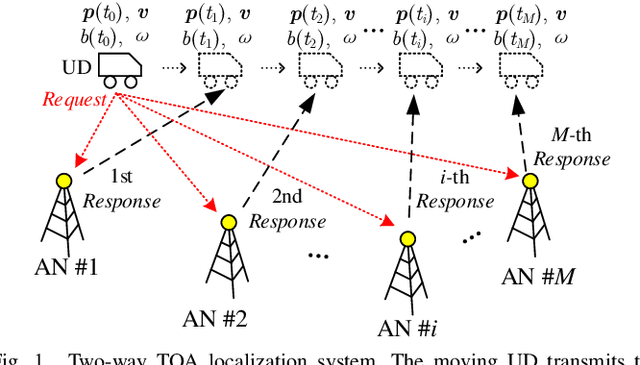
A two-way time-of-arrival (TOA system is composed of anchor nodes (ANs and user devices (UDs . Two-way TOA measurements between AN-UD pairs are obtained via round-trip communications to achieve localization and synchronization (LAS for a UD. Existing LAS method for a moving UD with clock drift adopts an iterative algorithm, which requires accurate initialization and has high computational complexity. In this paper, we propose a new closed-form two-way TOA LAS approach, namely CFTWLAS, which does not require initialization, has low complexity and empirically achieves optimal LAS accuracy. We first linearize the LAS problem by squaring and differencing the two-way TOA equations. We employ two auxiliary variables to simplify the problem to finding the analytical solution of quadratic equations. Due to the measurement noise, we can only obtain a raw LAS estimation from the solution of the auxiliary variables. Then, a weighted least squares step is applied to further refine the raw estimation. We analyze the theoretical error of the new CFTWLAS and show that it empirically reaches the Cramer-Rao lower bound (CRLB with sufficient ANs under the condition with proper geometry and small noise. Numerical results in a 3D scenario verify the theoretical analysis that the estimation accuracy of the new CFTWLAS method reaches CRLB in the presented experiments when the number of the ANs is large, the geometry is appropriate, and the noise is small. Unlike the iterative method whose complexity increases with the iteration count, the new CFTWLAS has constant low complexity.