Semidefinite Programming Two-way TOA Localization for User Devices with Motion and Clock Drift

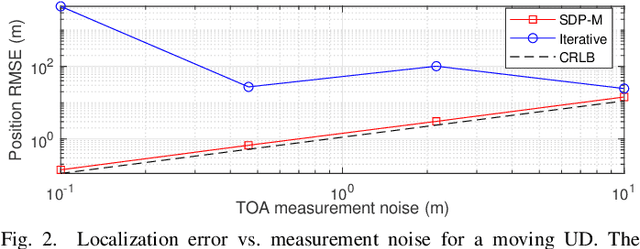
In two-way time-of-arrival (TOA) systems, a user device (UD) obtains its position by round-trip communications to a number of anchor nodes (ANs) at known locations. The objective function of the maximum likelihood (ML) method for two-way TOA localization is nonconvex. Thus, the widely-adopted Gauss-Newton iterative method to solve the ML estimator usually suffers from the local minima problem. In this paper, we convert the original estimator into a convex problem by relaxation, and develop a new semidefinite programming (SDP) based localization method for moving UDs, namely SDP-M. Numerical result demonstrates that compared with the iterative method, which often fall into local minima, the SDP-M always converge to the global optimal solution and significantly reduces the localization error by more than 40%. It also has stable localization accuracy regardless of the UD movement, and outperforms the conventional method for stationary UDs, which has larger error with growing UD velocity.