Optimal Localization with Sequential Pseudorange Measurements for Moving Users in a Time Division Broadcast Positioning System
Paper and Code
Feb 01, 2021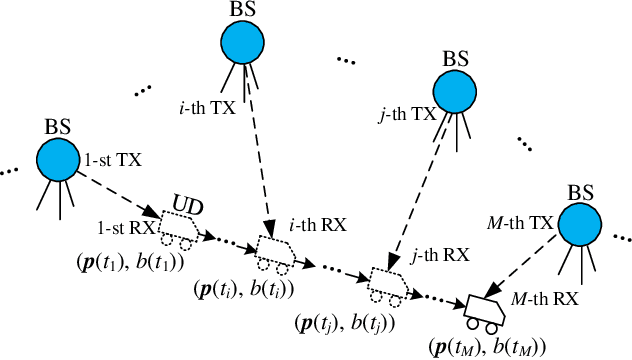

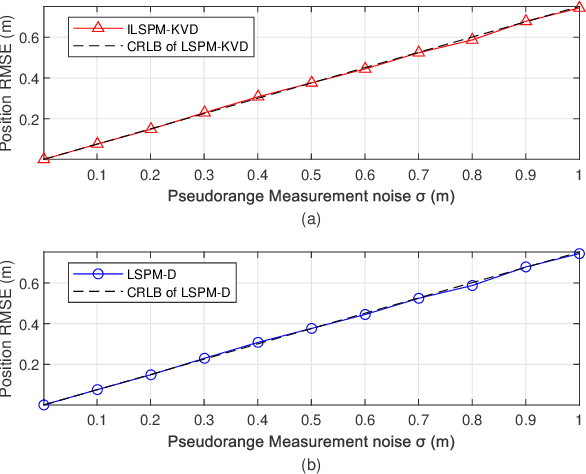
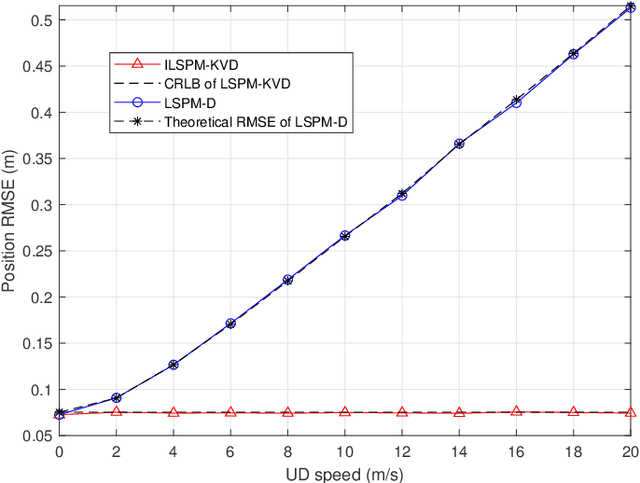
In a time division broadcast positioning system (TDBPS), a user device (UD) determines its position by obtaining sequential time-of-arrival (TOA) or pseudorange measurements from signals broadcast by multiple synchronized base stations (BSs). The existing localization method using sequential pseudorange measurements and a linear clock drift model for the TDPBS, namely LSPM-D, does not compensate the position displacement caused by the UD movement and will result in position error. In this paper, depending on the knowledge of the UD velocity, we develop a set of optimal localization methods for different cases. First, for known UD velocity, we develop the optimal localization method, namely LSPM-KVD, to compensate the movement-caused position error. We show that the LSPM-D is a special case of the LSPM-KVD when the UD is stationary with zero velocity. Second, for the case with unknown UD velocity, we develop a maximum likelihood (ML) method to jointly estimate the UD position and velocity, namely LSPM-UVD. Third, in the case that we have prior distribution information of the UD velocity, we present a maximum a posteriori (MAP) estimator for localization, namely LSPM-PVD. We derive the Cramer-Rao lower bound (CRLB) for all three estimators and analyze their localization error performance. We show that the position error of the LSPM-KVD increases as the assumed known velocity deviates from the true value. As expected, the LSPM-KVD has the smallest position error while the LSPM-PVD and the LSPM-UVD are more robust when the prior knowledge of the UD velocity is limited. Numerical results verify the theoretical analysis on the optimality and the positioning accuracy of the proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge