TANGLED: Generating 3D Hair Strands from Images with Arbitrary Styles and Viewpoints

Hairstyles are intricate and culturally significant with various geometries, textures, and structures. Existing text or image-guided generation methods fail to handle the richness and complexity of diverse styles. We present TANGLED, a novel approach for 3D hair strand generation that accommodates diverse image inputs across styles, viewpoints, and quantities of input views. TANGLED employs a three-step pipeline. First, our MultiHair Dataset provides 457 diverse hairstyles annotated with 74 attributes, emphasizing complex and culturally significant styles to improve model generalization. Second, we propose a diffusion framework conditioned on multi-view linearts that can capture topological cues (e.g., strand density and parting lines) while filtering out noise. By leveraging a latent diffusion model with cross-attention on lineart features, our method achieves flexible and robust 3D hair generation across diverse input conditions. Third, a parametric post-processing module enforces braid-specific constraints to maintain coherence in complex structures. This framework not only advances hairstyle realism and diversity but also enables culturally inclusive digital avatars and novel applications like sketch-based 3D strand editing for animation and augmented reality.

GaussianHair: Hair Modeling and Rendering with Light-aware Gaussians

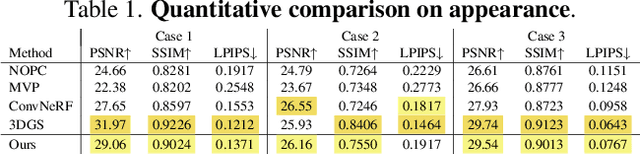
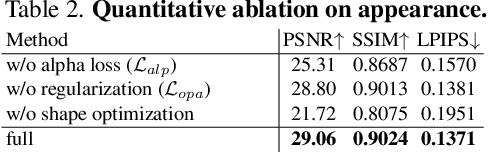
Hairstyle reflects culture and ethnicity at first glance. In the digital era, various realistic human hairstyles are also critical to high-fidelity digital human assets for beauty and inclusivity. Yet, realistic hair modeling and real-time rendering for animation is a formidable challenge due to its sheer number of strands, complicated structures of geometry, and sophisticated interaction with light. This paper presents GaussianHair, a novel explicit hair representation. It enables comprehensive modeling of hair geometry and appearance from images, fostering innovative illumination effects and dynamic animation capabilities. At the heart of GaussianHair is the novel concept of representing each hair strand as a sequence of connected cylindrical 3D Gaussian primitives. This approach not only retains the hair's geometric structure and appearance but also allows for efficient rasterization onto a 2D image plane, facilitating differentiable volumetric rendering. We further enhance this model with the "GaussianHair Scattering Model", adept at recreating the slender structure of hair strands and accurately capturing their local diffuse color in uniform lighting. Through extensive experiments, we substantiate that GaussianHair achieves breakthroughs in both geometric and appearance fidelity, transcending the limitations encountered in state-of-the-art methods for hair reconstruction. Beyond representation, GaussianHair extends to support editing, relighting, and dynamic rendering of hair, offering seamless integration with conventional CG pipeline workflows. Complementing these advancements, we have compiled an extensive dataset of real human hair, each with meticulously detailed strand geometry, to propel further research in this field.

Supervised Kernel PCA For Longitudinal Data

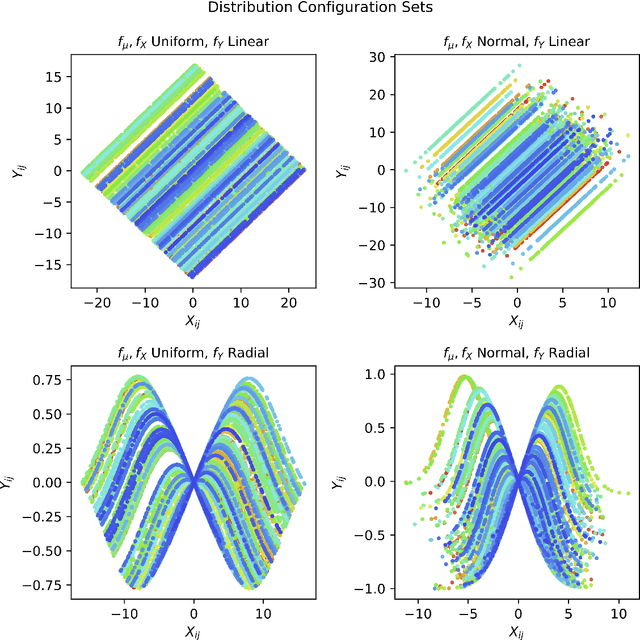
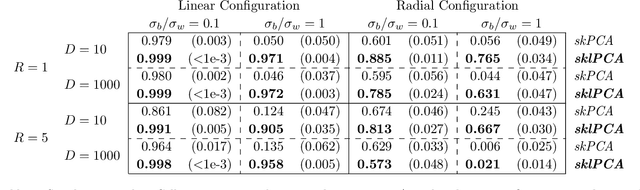
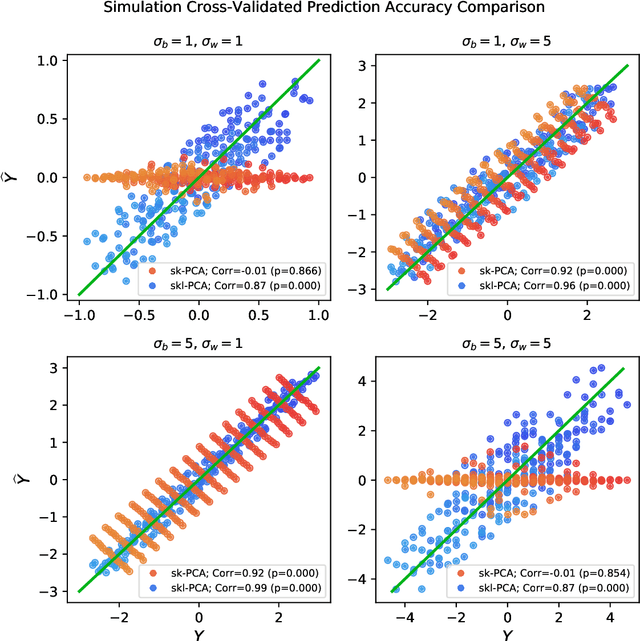
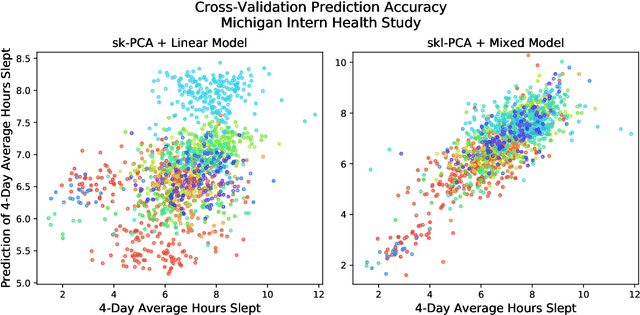
In statistical learning, high covariate dimensionality poses challenges for robust prediction and inference. To address this challenge, supervised dimension reduction is often performed, where dependence on the outcome is maximized for a selected covariate subspace with smaller dimensionality. Prevalent dimension reduction techniques assume data are $i.i.d.$, which is not appropriate for longitudinal data comprising multiple subjects with repeated measurements over time. In this paper, we derive a decomposition of the Hilbert-Schmidt Independence Criterion as a supervised loss function for longitudinal data, enabling dimension reduction between and within clusters separately, and propose a dimensionality-reduction technique, $sklPCA$, that performs this decomposed dimension reduction. We also show that this technique yields superior model accuracy compared to the model it extends.