Supervised Kernel PCA For Longitudinal Data

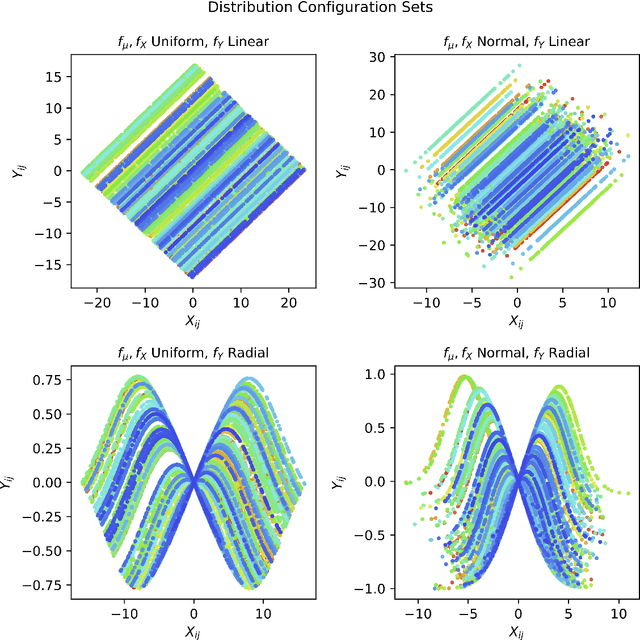
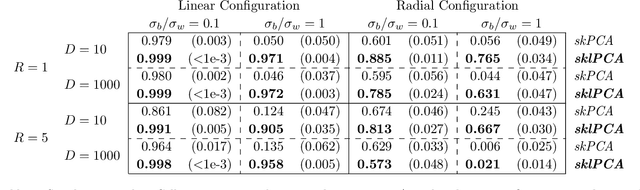
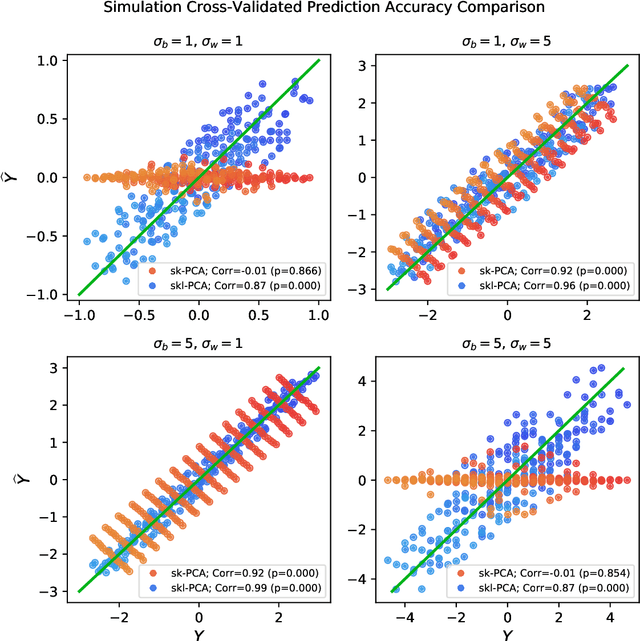
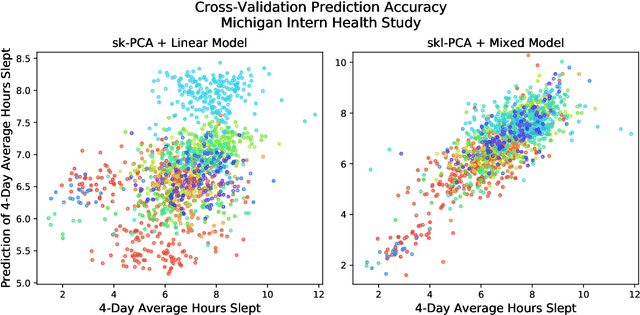
In statistical learning, high covariate dimensionality poses challenges for robust prediction and inference. To address this challenge, supervised dimension reduction is often performed, where dependence on the outcome is maximized for a selected covariate subspace with smaller dimensionality. Prevalent dimension reduction techniques assume data are $i.i.d.$, which is not appropriate for longitudinal data comprising multiple subjects with repeated measurements over time. In this paper, we derive a decomposition of the Hilbert-Schmidt Independence Criterion as a supervised loss function for longitudinal data, enabling dimension reduction between and within clusters separately, and propose a dimensionality-reduction technique, $sklPCA$, that performs this decomposed dimension reduction. We also show that this technique yields superior model accuracy compared to the model it extends.

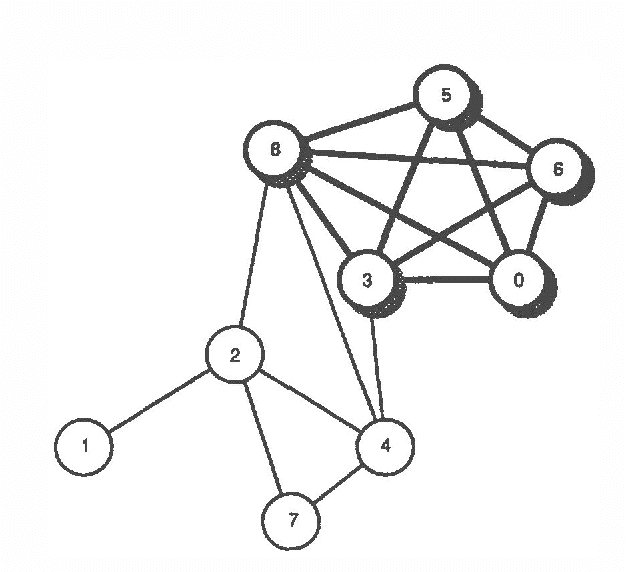
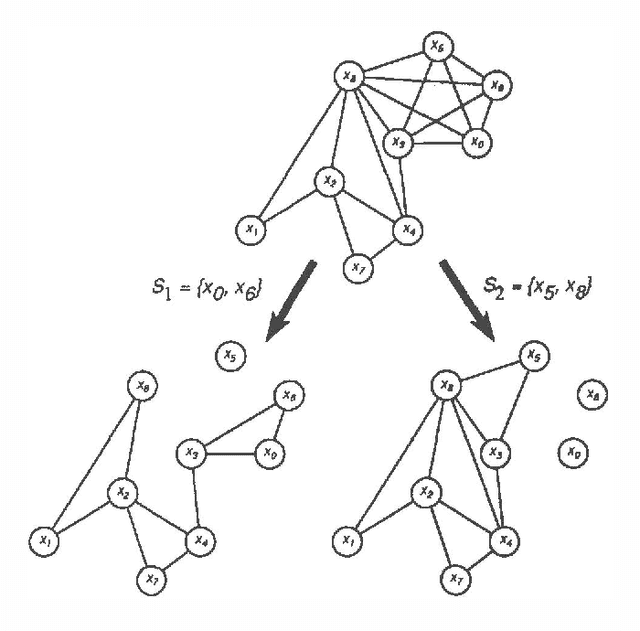
Reformulating Inference Problems Through Selective Conditioning

We describe how we selectively reformulate portions of a belief network that pose difficulties for solution with a stochastic-simulation algorithm. With employ the selective conditioning approach to target specific nodes in a belief network for decomposition, based on the contribution the nodes make to the tractability of stochastic simulation. We review previous work on BNRAS algorithms- randomized approximation algorithms for probabilistic inference. We show how selective conditioning can be employed to reformulate a single BNRAS problem into multiple tractable BNRAS simulation problems. We discuss how we can use another simulation algorithm-logic sampling-to solve a component of the inference problem that provides a means for knitting the solutions of individual subproblems into a final result. Finally, we analyze tradeoffs among the computational subtasks associated with the selective conditioning approach to reformulation.

Dynamic Network Models for Forecasting

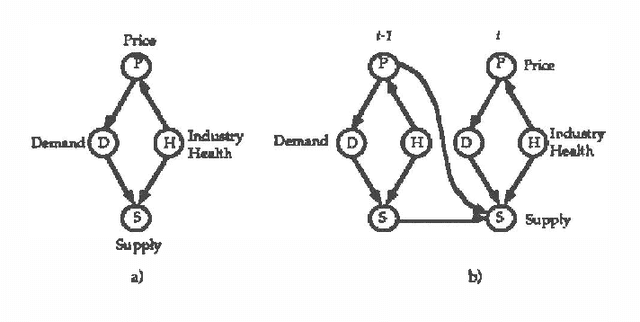
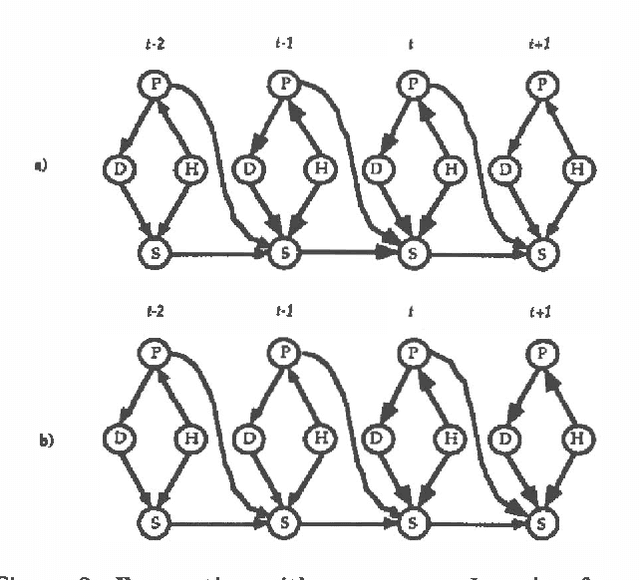
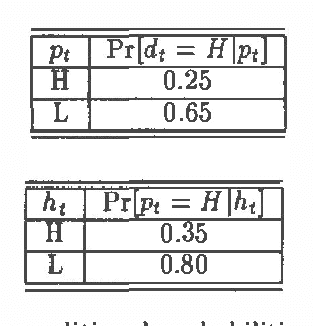
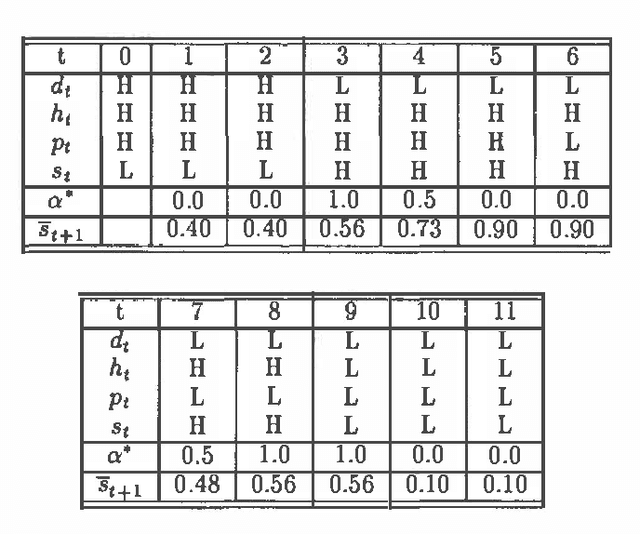
We have developed a probabilistic forecasting methodology through a synthesis of belief network models and classical time-series analysis. We present the dynamic network model (DNM) and describe methods for constructing, refining, and performing inference with this representation of temporal probabilistic knowledge. The DNM representation extends static belief-network models to more general dynamic forecasting models by integrating and iteratively refining contemporaneous and time-lagged dependencies. We discuss key concepts in terms of a model for forecasting U.S. car sales in Japan.

Additive Belief-Network Models

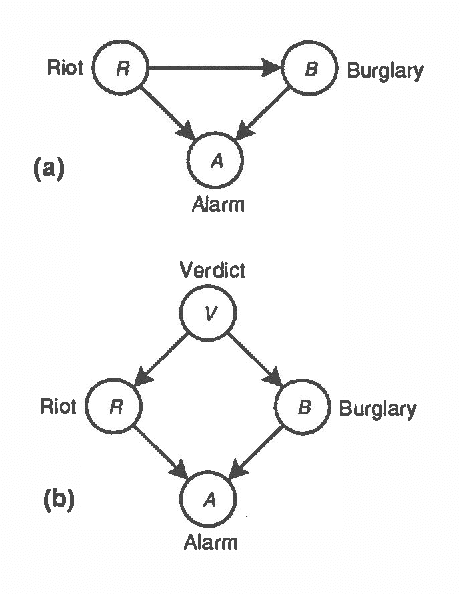
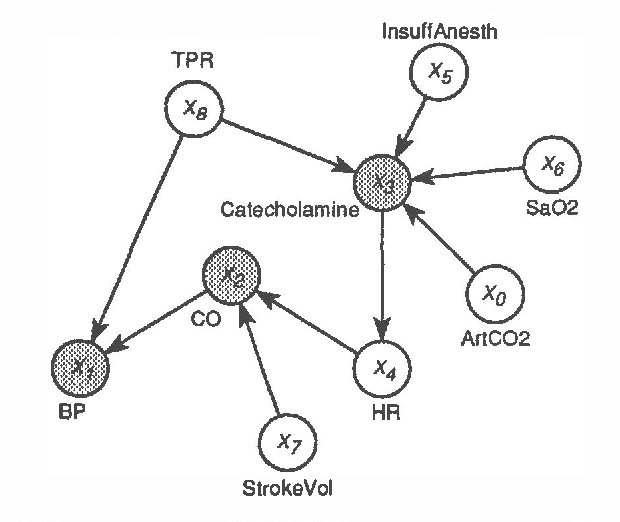
The inherent intractability of probabilistic inference has hindered the application of belief networks to large domains. Noisy OR-gates [30] and probabilistic similarity networks [18, 17] escape the complexity of inference by restricting model expressiveness. Recent work in the application of belief-network models to time-series analysis and forecasting [9, 10] has given rise to the additive belief network model (ABNM). We (1) discuss the nature and implications of the approximations made by an additive decomposition of a belief network, (2) show greater efficiency in the induction of additive models when available data are scarce, (3) generalize probabilistic inference algorithms to exploit the additive decomposition of ABNMs, (4) show greater efficiency of inference, and (5) compare results on inference with a simple additive belief network.

Forecasting Sleep Apnea with Dynamic Network Models

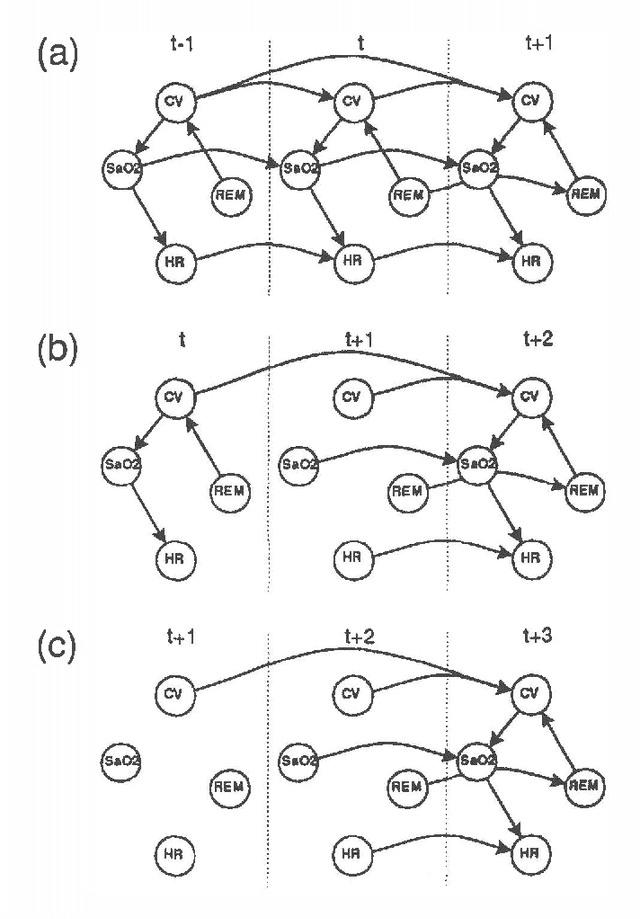
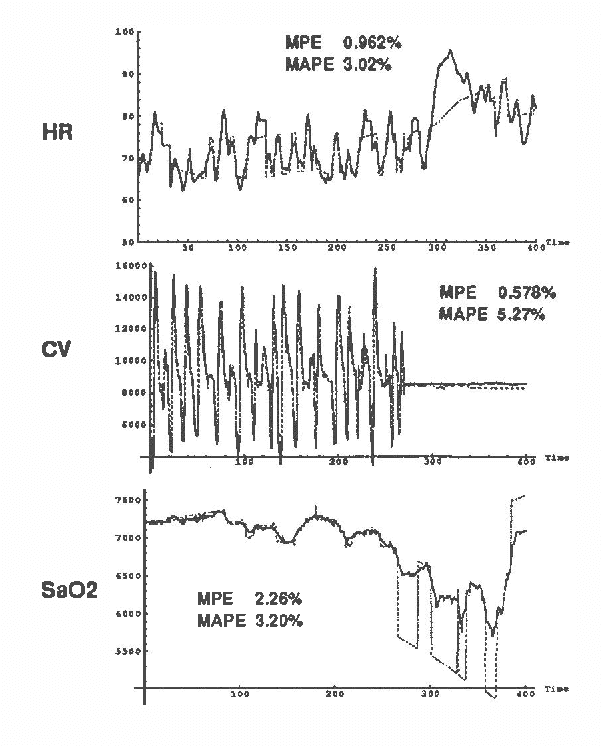
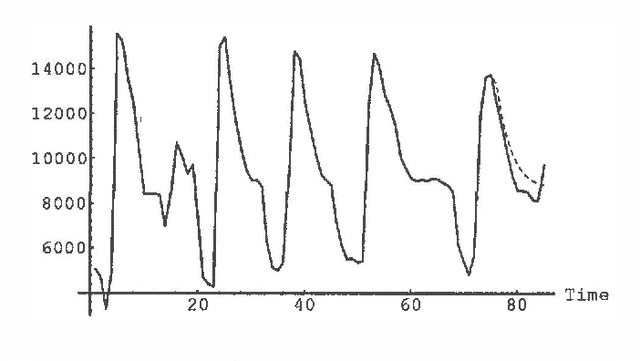
Dynamic network models (DNMs) are belief networks for temporal reasoning. The DNM methodology combines techniques from time series analysis and probabilistic reasoning to provide (1) a knowledge representation that integrates noncontemporaneous and contemporaneous dependencies and (2) methods for iteratively refining these dependencies in response to the effects of exogenous influences. We use belief-network inference algorithms to perform forecasting, control, and discrete event simulation on DNMs. The belief network formulation allows us to move beyond the traditional assumptions of linearity in the relationships among time-dependent variables and of normality in their probability distributions. We demonstrate the DNM methodology on an important forecasting problem in medicine. We conclude with a discussion of how the methodology addresses several limitations found in traditional time series analyses.

Optimal Monte Carlo Estimation of Belief Network Inference

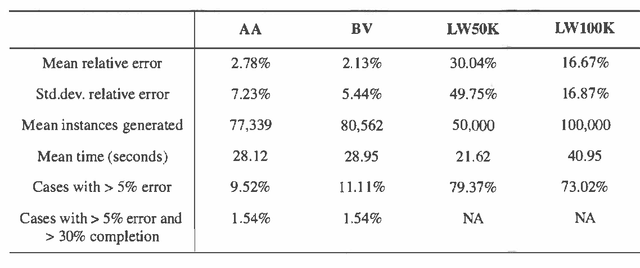
We present two Monte Carlo sampling algorithms for probabilistic inference that guarantee polynomial-time convergence for a larger class of network than current sampling algorithms provide. These new methods are variants of the known likelihood weighting algorithm. We use of recent advances in the theory of optimal stopping rules for Monte Carlo simulation to obtain an inference approximation with relative error epsilon and a small failure probability delta. We present an empirical evaluation of the algorithms which demonstrates their improved performance.