Dynamic Network Models for Forecasting

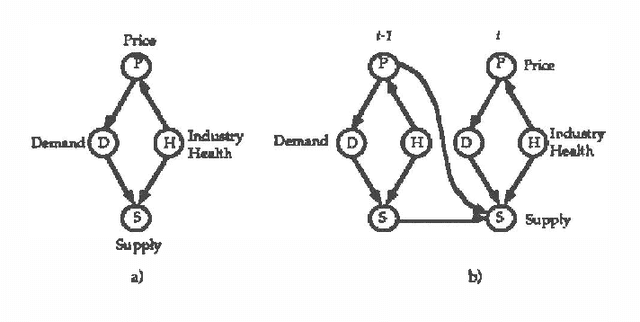
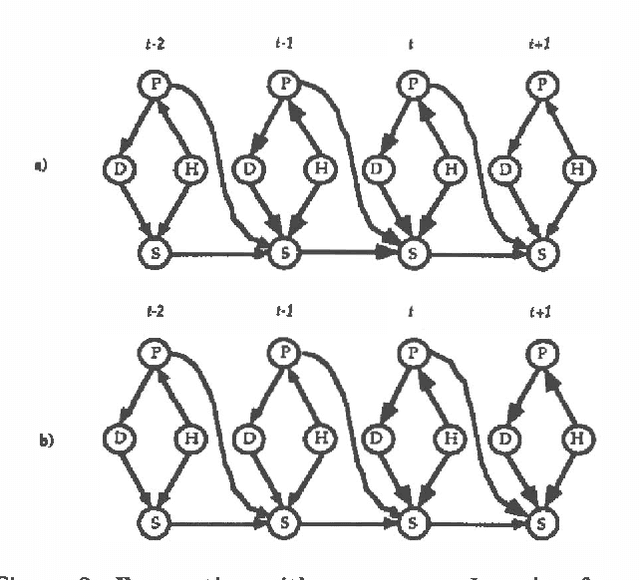
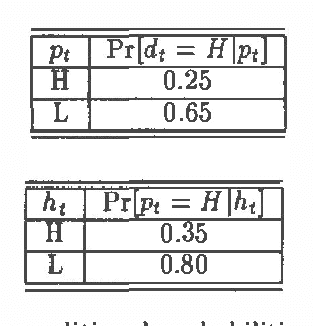
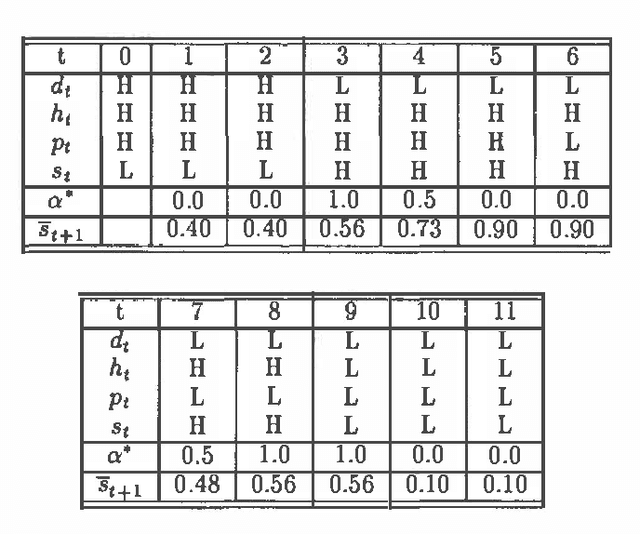
We have developed a probabilistic forecasting methodology through a synthesis of belief network models and classical time-series analysis. We present the dynamic network model (DNM) and describe methods for constructing, refining, and performing inference with this representation of temporal probabilistic knowledge. The DNM representation extends static belief-network models to more general dynamic forecasting models by integrating and iteratively refining contemporaneous and time-lagged dependencies. We discuss key concepts in terms of a model for forecasting U.S. car sales in Japan.

Additive Belief-Network Models

The inherent intractability of probabilistic inference has hindered the application of belief networks to large domains. Noisy OR-gates [30] and probabilistic similarity networks [18, 17] escape the complexity of inference by restricting model expressiveness. Recent work in the application of belief-network models to time-series analysis and forecasting [9, 10] has given rise to the additive belief network model (ABNM). We (1) discuss the nature and implications of the approximations made by an additive decomposition of a belief network, (2) show greater efficiency in the induction of additive models when available data are scarce, (3) generalize probabilistic inference algorithms to exploit the additive decomposition of ABNMs, (4) show greater efficiency of inference, and (5) compare results on inference with a simple additive belief network.

Forecasting Sleep Apnea with Dynamic Network Models

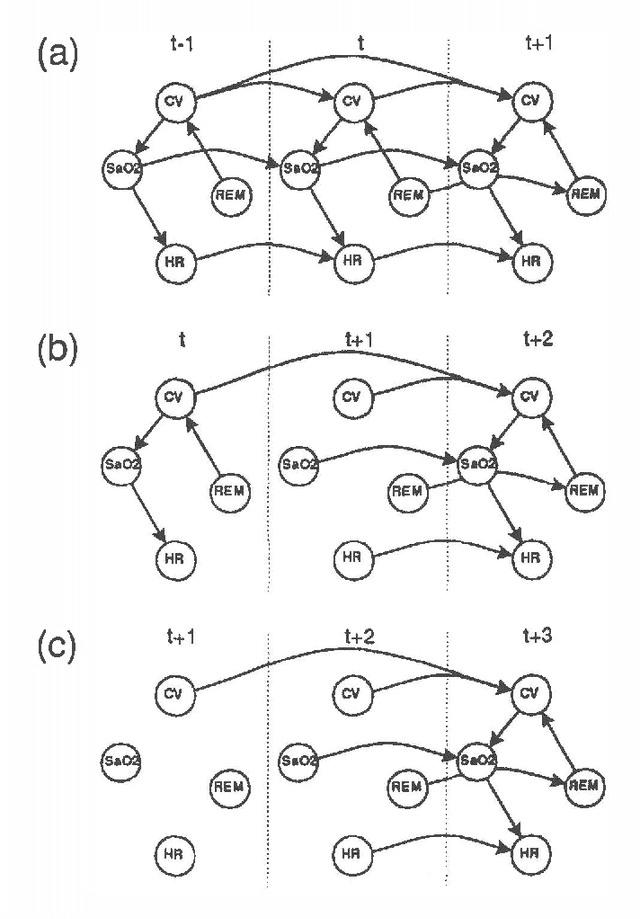
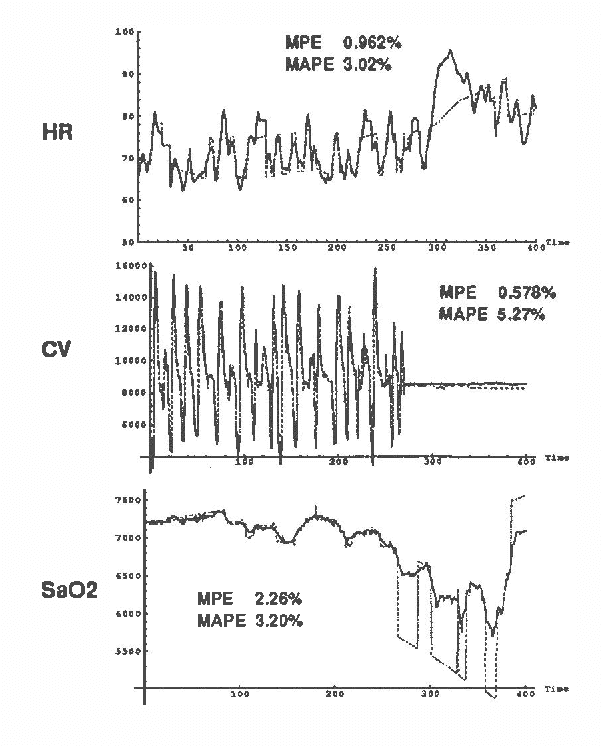
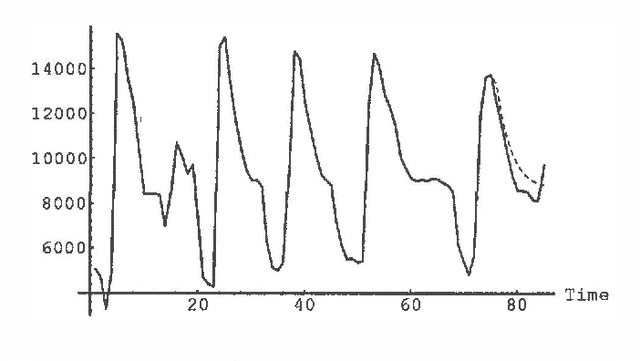
Dynamic network models (DNMs) are belief networks for temporal reasoning. The DNM methodology combines techniques from time series analysis and probabilistic reasoning to provide (1) a knowledge representation that integrates noncontemporaneous and contemporaneous dependencies and (2) methods for iteratively refining these dependencies in response to the effects of exogenous influences. We use belief-network inference algorithms to perform forecasting, control, and discrete event simulation on DNMs. The belief network formulation allows us to move beyond the traditional assumptions of linearity in the relationships among time-dependent variables and of normality in their probability distributions. We demonstrate the DNM methodology on an important forecasting problem in medicine. We conclude with a discussion of how the methodology addresses several limitations found in traditional time series analyses.