Supervised Kernel PCA For Longitudinal Data
Paper and Code
Aug 23, 2018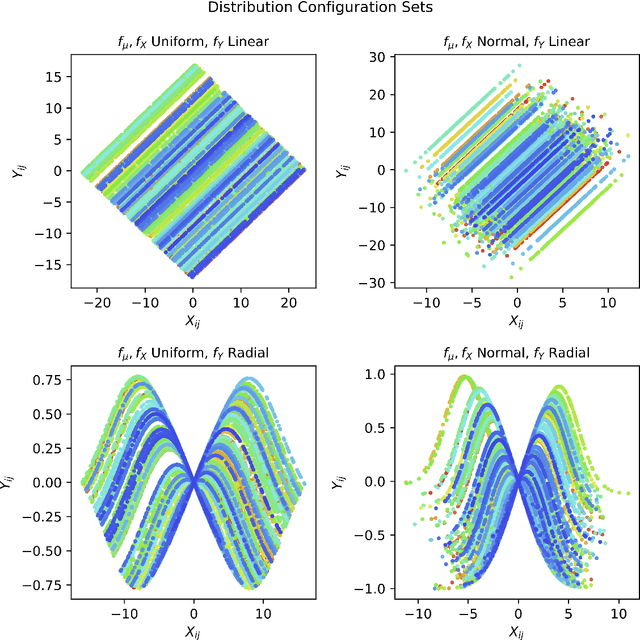
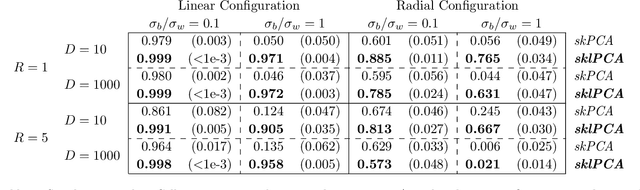
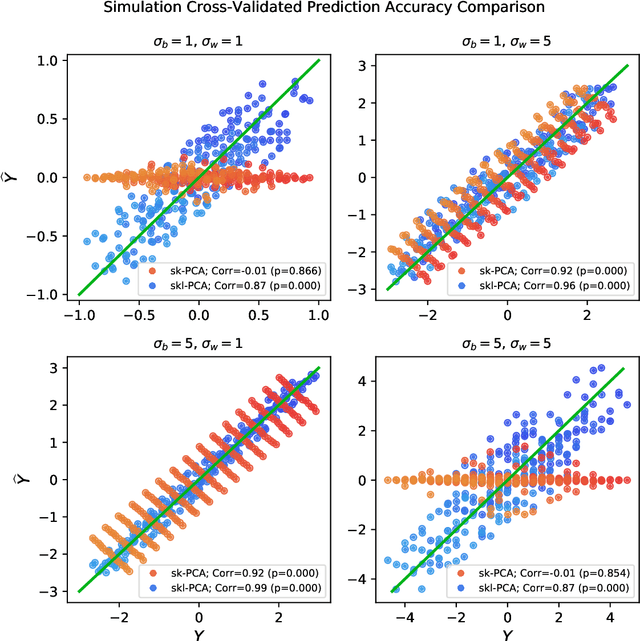
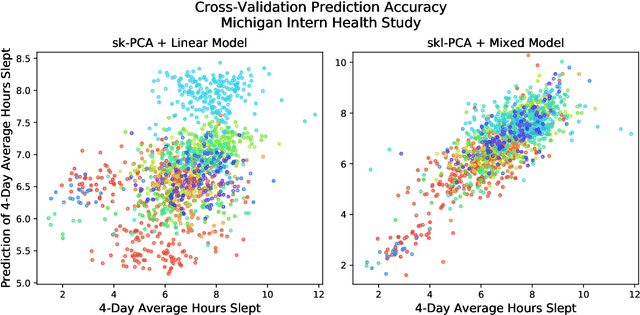
In statistical learning, high covariate dimensionality poses challenges for robust prediction and inference. To address this challenge, supervised dimension reduction is often performed, where dependence on the outcome is maximized for a selected covariate subspace with smaller dimensionality. Prevalent dimension reduction techniques assume data are $i.i.d.$, which is not appropriate for longitudinal data comprising multiple subjects with repeated measurements over time. In this paper, we derive a decomposition of the Hilbert-Schmidt Independence Criterion as a supervised loss function for longitudinal data, enabling dimension reduction between and within clusters separately, and propose a dimensionality-reduction technique, $sklPCA$, that performs this decomposed dimension reduction. We also show that this technique yields superior model accuracy compared to the model it extends.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge