Novel Sparse Recovery Algorithms for 3D Debris Localization using Rotating Point Spread Function Imagery

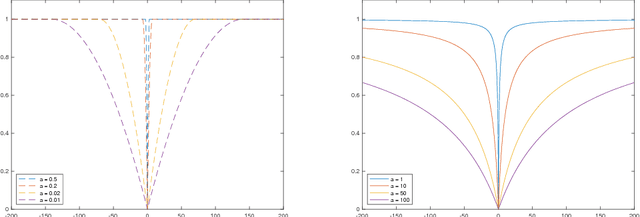
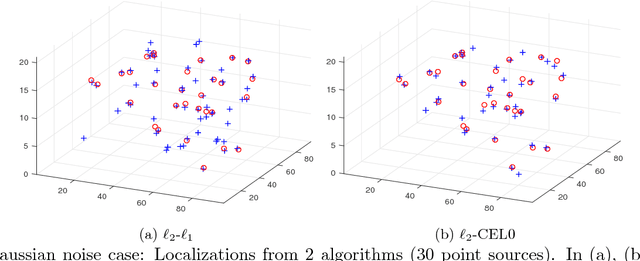
An optical imager that exploits off-center image rotation to encode both the lateral and depth coordinates of point sources in a single snapshot can perform 3D localization and tracking of space debris. When actively illuminated, unresolved space debris, which can be regarded as a swarm of point sources, can scatter a fraction of laser irradiance back into the imaging sensor. Determining the source locations and fluxes is a large-scale sparse 3D inverse problem, for which we have developed efficient and effective algorithms based on sparse recovery using non-convex optimization. Numerical simulations illustrate the efficiency and stability of the algorithms.

A Nonlocal Denoising Algorithm for Manifold-Valued Images Using Second Order Statistics

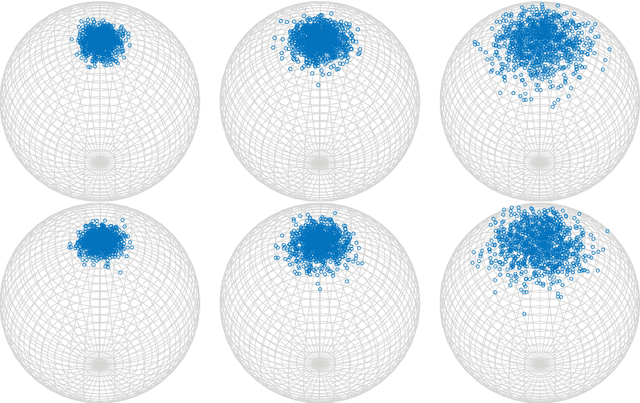
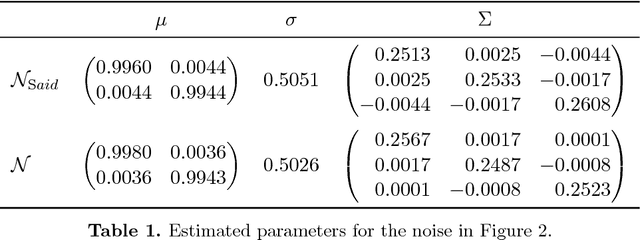
Nonlocal patch-based methods, in particular the Bayes' approach of Lebrun, Buades and Morel (2013), are considered as state-of-the-art methods for denoising (color) images corrupted by white Gaussian noise of moderate variance. This paper is the first attempt to generalize this technique to manifold-valued images. Such images, for example images with phase or directional entries or with values in the manifold of symmetric positive definite matrices, are frequently encountered in real-world applications. Generalizing the normal law to manifolds is not canonical and different attempts have been considered. Here we focus on a straightforward intrinsic model and discuss the relation to other approaches for specific manifolds. We reinterpret the Bayesian approach of Lebrun et al. (2013) in terms of minimum mean squared error estimation, which motivates our definition of a corresponding estimator on the manifold. With this estimator at hand we present a nonlocal patch-based method for the restoration of manifold-valued images. Various proof of concept examples demonstrate the potential of the proposed algorithm.

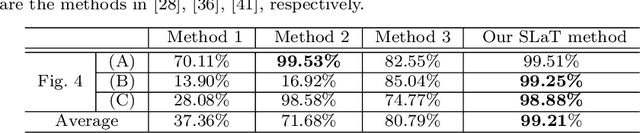
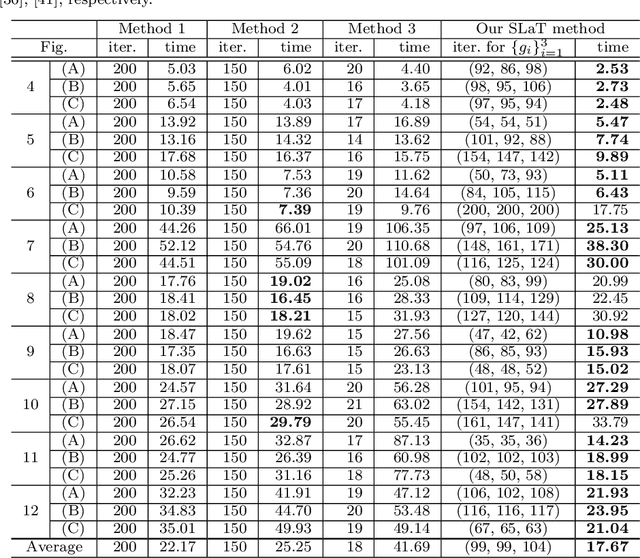
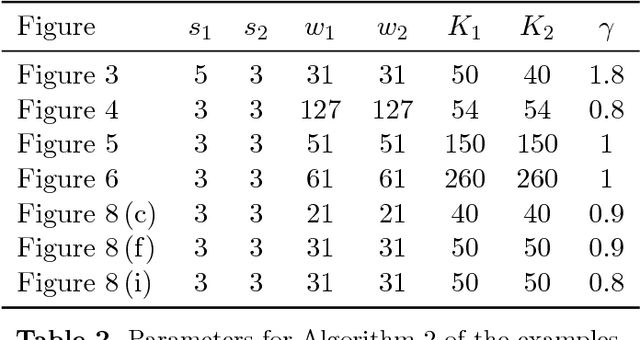
A Three-stage Approach for Segmenting Degraded Color Images: Smoothing, Lifting and Thresholding (SLaT)

In this paper, we propose a SLaT (Smoothing, Lifting and Thresholding) method with three stages for multiphase segmentation of color images corrupted by different degradations: noise, information loss, and blur. At the first stage, a convex variant of the Mumford-Shah model is applied to each channel to obtain a smooth image. We show that the model has unique solution under the different degradations. In order to properly handle the color information, the second stage is dimension lifting where we consider a new vector-valued image composed of the restored image and its transform in the secondary color space with additional information. This ensures that even if the first color space has highly correlated channels, we can still have enough information to give good segmentation results. In the last stage, we apply multichannel thresholding to the combined vector-valued image to find the segmentation. The number of phases is only required in the last stage, so users can choose or change it all without the need of solving the previous stages again. Experiments demonstrate that our SLaT method gives excellent results in terms of segmentation quality and CPU time in comparison with other state-of-the-art segmentation methods.