A Nonlocal Denoising Algorithm for Manifold-Valued Images Using Second Order Statistics
Paper and Code
Dec 12, 2016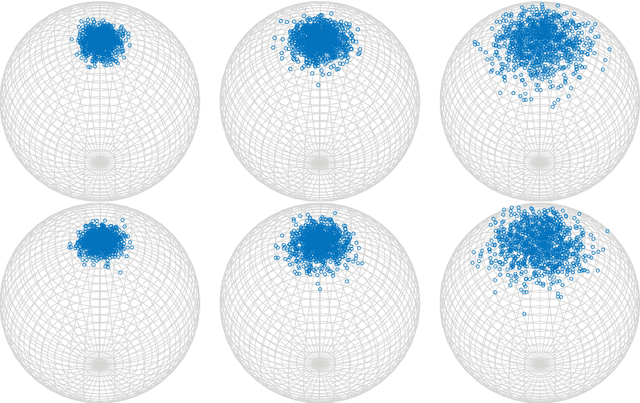
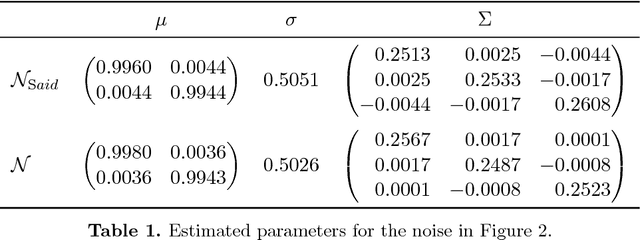
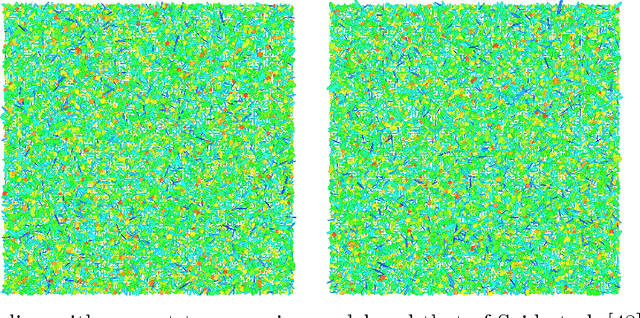
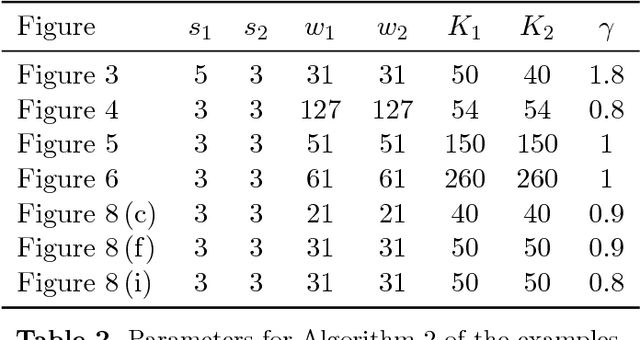
Nonlocal patch-based methods, in particular the Bayes' approach of Lebrun, Buades and Morel (2013), are considered as state-of-the-art methods for denoising (color) images corrupted by white Gaussian noise of moderate variance. This paper is the first attempt to generalize this technique to manifold-valued images. Such images, for example images with phase or directional entries or with values in the manifold of symmetric positive definite matrices, are frequently encountered in real-world applications. Generalizing the normal law to manifolds is not canonical and different attempts have been considered. Here we focus on a straightforward intrinsic model and discuss the relation to other approaches for specific manifolds. We reinterpret the Bayesian approach of Lebrun et al. (2013) in terms of minimum mean squared error estimation, which motivates our definition of a corresponding estimator on the manifold. With this estimator at hand we present a nonlocal patch-based method for the restoration of manifold-valued images. Various proof of concept examples demonstrate the potential of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge