A Versatile Low-Complexity Feedback Scheme for FDD Systems via Generative Modeling

In this work, we propose a versatile feedback scheme which can be deployed for both single- and multi-user multiple-input multiple-output (MIMO) frequency division duplex (FDD) systems. Particularly, we propose to use a Gaussian mixture model (GMM) with a reduced number of parameters for codebook construction, feedback encoding, and precoder design. The GMM is fitted offline at the base station (BS) to uplink (UL) training samples to approximate the channel distribution of all possible mobile terminals (MTs) located inside the BS cell. Afterwards, a codebook is constructed, where each codebook entry is based on one GMM component. By extracting directional information of the constructed codebook, the proposed GMM-based feedback approach allows to jointly design the precoders of a multi-user MIMO (MU-MIMO) system using common precoding algorithms. Alternatively, the GMM's sample generation ability can be utilized to design the precoders using a state-of-the-art stochastic iterative algorithm. After offloading the GMM to the MTs, they determine their feedback simply as the index of the GMM component with the highest responsibility for their received pilot signal. This strategy exhibits low complexity and allows for parallelization. Simulation results show that the proposed approach outperforms conventional methods, especially for a reduced number of pilots.

On the Mean Square Error Optimal Estimator in One-Bit Quantized Systems

This paper investigates the mean square error (MSE)-optimal conditional mean estimator (CME) in one-bit quantized systems in the context of channel estimation with jointly Gaussian inputs. We analyze the relationship of the generally nonlinear CME to the linear Bussgang estimator, a well-known method based on Bussgang's theorem. We highlight a novel observation that the Bussgang estimator is equal to the CME for different special cases, including the case of univariate Gaussian inputs and the case of multiple observations in the absence of additive noise prior to the quantization. For the general cases we conduct numerical simulations to quantify the gap between the Bussgang estimator and the CME. This gap increases for higher dimensions and longer pilot sequences. We propose an optimal pilot sequence, motivated by insights from the CME, and derive a novel closed-form expression of the MSE for that case. Afterwards, we find a closed-form limit of the MSE in the asymptotically large number of pilots regime that also holds for the Bussgang estimator. Lastly, we present numerical experiments for various system parameters and for different performance metrics which illuminate the behavior of the optimal channel estimator in the quantized regime. In this context, the well-known stochastic resonance effect that appears in quantized systems can be quantified.

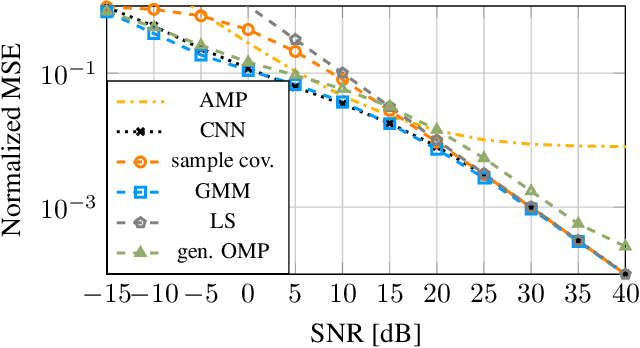
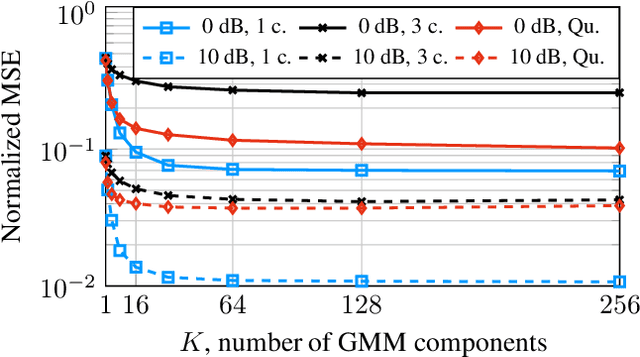
Evaluation of a Gaussian Mixture Model-based Channel Estimator using Measurement Data

In this work, we use real-world data in order to evaluate and validate a machine learning (ML)-based algorithm for physical layer functionalities. Specifically, we apply a recently introduced Gaussian mixture model (GMM)-based algorithm in order to estimate uplink channels stemming from a measurement campaign. For this estimator, there is an initial (offline) training phase, where a GMM is fitted onto given channel (training) data. Thereafter, the fitted GMM is used for (online) channel estimation. Our experiments suggest that the GMM estimator learns the intrinsic characteristics of a given base station's whole radio propagation environment. Essentially, this ambient information is captured due to universal approximation properties of the initially fitted GMM. For a large enough number of GMM components, the GMM estimator was shown to approximate the (unknown) mean squared error (MSE)-optimal channel estimator arbitrarily well. In our experiments, the GMM estimator shows significant performance gains compared to approaches that are not able to capture the ambient information. To validate the claim that ambient information is learnt, we generate synthetic channel data using a state-of-the-art channel simulator and train the GMM estimator once on these and once on the real data, and we apply the estimator once to the synthetic and once to the real data. We then observe how providing suitable ambient information in the training phase beneficially impacts the later channel estimation performance.

GMM-based Codebook Construction and Feedback Encoding in FDD Systems

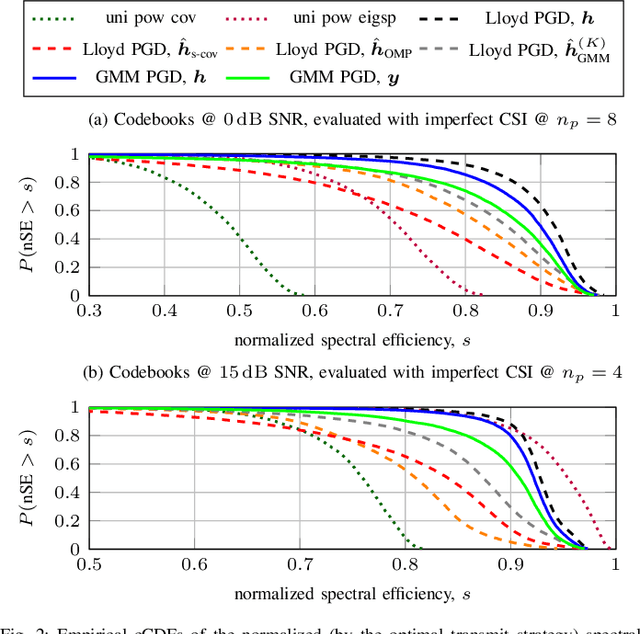
We propose a precoder codebook construction and feedback encoding scheme which is based on Gaussian mixture models (GMMs). In an offline phase, the base station (BS) first fits a GMM to uplink (UL) training samples. Thereafter, it designs a codebook in an unsupervised manner by exploiting the GMM's clustering capability. We design one codebook entry per GMM component. After offloading the GMM-but not the codebook-to the mobile terminal (MT) in the online phase, the MT utilizes the GMM to determine the best fitting codebook entry. To this end, no channel estimation is necessary at the MT. Instead, the MT's observed signal is used to evaluate how responsible each component of the GMM is for the signal. The feedback consists of the index of the GMM component with the highest responsibility and the BS then employs the corresponding codebook entry. Simulation results show that the proposed codebook design and feedback encoding scheme outperforms conventional Lloyd clustering based codebook design algorithms, especially in configurations with reduced pilot overhead.

Variational Autoencoder Leveraged MMSE Channel Estimation

We propose to utilize a variational autoencoder (VAE) for data-driven channel estimation. The underlying true and unknown channel distribution is modeled by the VAE as a conditional Gaussian distribution in a novel way, parameterized by the respective first and second order conditional moments. As a result, it can be observed that the linear minimum mean square error (LMMSE) estimator in its variant conditioned on the latent sample of the VAE approximates an optimal MSE estimator. Furthermore, we argue how a VAE-based channel estimator can approximate the MMSE channel estimator. We propose three variants of VAE estimators that differ in the data used during training and estimation. First, we show that given perfectly known channel state information at the input of the VAE during estimation, which is impractical, we obtain an estimator that can serve as a benchmark result for an estimation scenario. We then propose practically feasible approaches, where perfectly known channel state information is only necessary in the training phase or is not needed at all. Simulation results on 3GPP and QuaDRiGa channel data attest a small performance loss of the practical approaches and the superiority of our VAE approaches in comparison to other related channel estimation methods.

Channel Estimation based on Gaussian Mixture Models with Structured Covariances

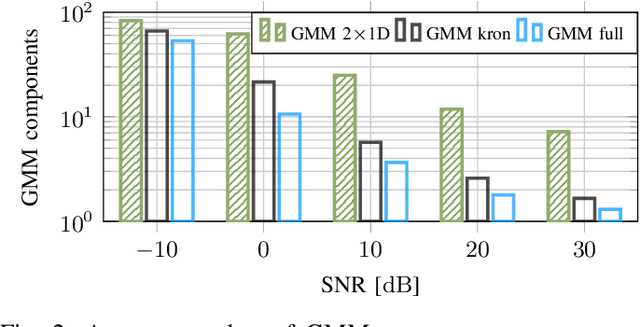
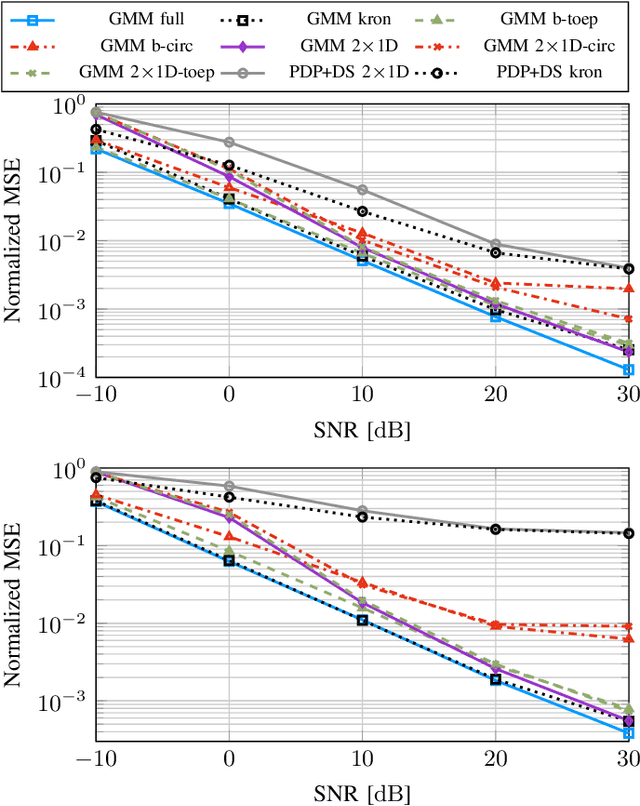
In this work, we propose variations of a Gaussian mixture model (GMM) based channel estimator that was recently proven to be asymptotically optimal in the minimum mean square error (MMSE) sense. We account for the need of low computational complexity in the online estimation and low cost for training and storage in practical applications. To this end, we discuss modifications of the underlying expectation-maximization (EM) algorithm, which is needed to fit the parameters of the GMM, to allow for structurally constrained covariances. Further, we investigate splitting the 2D time and frequency estimation problem in wideband systems into cascaded 1D estimations with the help of the GMM. The proposed cascaded GMM approach drastically reduces the complexity and memory requirements. We observe that due to the training on realistic channel data, the proposed GMM estimators seem to inherently perform a trade-off between saving complexity/parameters and estimation performance. We compare these low-complexity approaches to a practical and low cost method that relies on the power delay profile (PDP) and the Doppler spectrum (DS). We argue that, with the training on scenario-specific data from the environment, these practical baselines are outperformed by far with equal estimation complexity.

An Asymptotically Optimal Approximation of the Conditional Mean Channel Estimator based on Gaussian Mixture Models

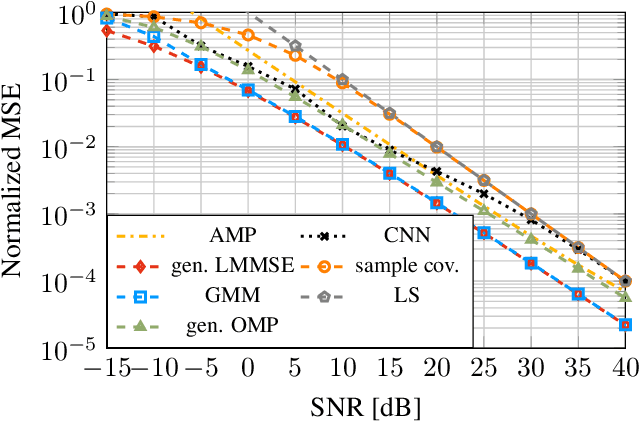
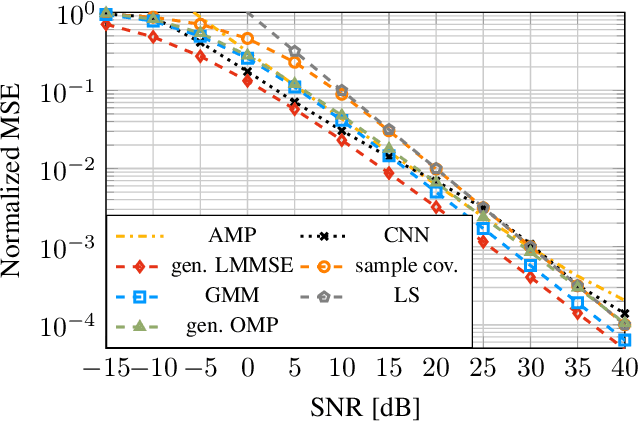
This paper investigates a channel estimator based on Gaussian mixture models (GMMs) in the context of linear inverse problems with additive Gaussian noise. We fit a GMM to given channel samples to obtain an analytic probability density function (PDF) which approximates the true channel PDF. Then, a conditional mean estimator (CME) corresponding to this approximating PDF is computed in closed form and used as an approximation of the optimal CME based on the true channel PDF. This optimal CME cannot be calculated analytically because the true channel PDF is generally unknown. We present mild conditions which allow us to prove the convergence of the GMM-based CME to the optimal CME as the number of GMM components is increased. Additionally, we investigate the estimator's computational complexity and present simplifications based on common model-based insights. Further, we study the estimator's behavior in numerical experiments including multiple-input multiple-output (MIMO) and wideband systems.

CSI Clustering with Variational Autoencoding

The model order of a wireless channel plays an important role for a variety of applications in communications engineering, e.g., it represents the number of resolvable incident wavefronts with non-negligible power incident from a transmitter to a receiver. Areas such as direction of arrival estimation leverage the model order to analyze the multipath components of channel state information. In this work, we propose to use a variational autoencoder to group unlabeled channel state information with respect to the model order in the variational autoencoder latent space in an unsupervised manner. We validate our approach with simulated 3GPP channel data. Our results suggest that, in order to learn an appropriate clustering, it is crucial to use a more flexible likelihood model for the variational autoencoder decoder than it is usually the case in standard applications.

Learning a Compressive Sensing Matrix with Structural Constraints via Maximum Mean Discrepancy Optimization

We introduce a learning-based algorithm to obtain a measurement matrix for compressive sensing related recovery problems. The focus lies on matrices with a constant modulus constraint which typically represent a network of analog phase shifters in hybrid precoding/combining architectures. We interpret a matrix with restricted isometry property as a mapping of points from a high- to a low-dimensional hypersphere. We argue that points on the low-dimensional hypersphere, namely, in the range of the matrix, should be uniformly distributed to increase robustness against measurement noise. This notion is formalized in an optimization problem which uses one of the maximum mean discrepancy metrics in the objective function. Recent success of such metrics in neural network related topics motivate a solution of the problem based on machine learning. Numerical experiments show better performance than random measurement matrices that are generally employed in compressive sensing contexts. Further, we adapt a method from the literature to the constant modulus constraint. This method can also compete with random matrices and it is shown to harmonize well with the proposed learning-based approach if it is used as an initialization. Lastly, we describe how other structural matrix constraints, e.g., a Toeplitz constraint, can be taken into account, too.

Unsupervised Learning of Adaptive Codebooks for Deep Feedback Encoding in FDD Systems

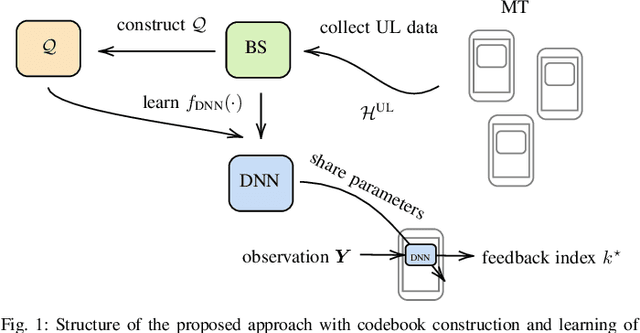
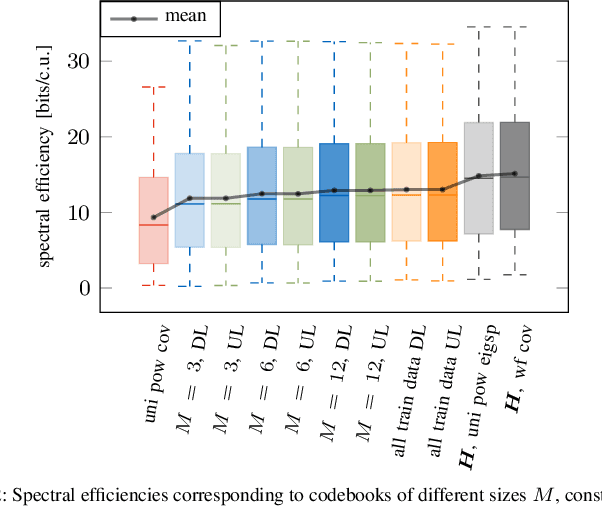
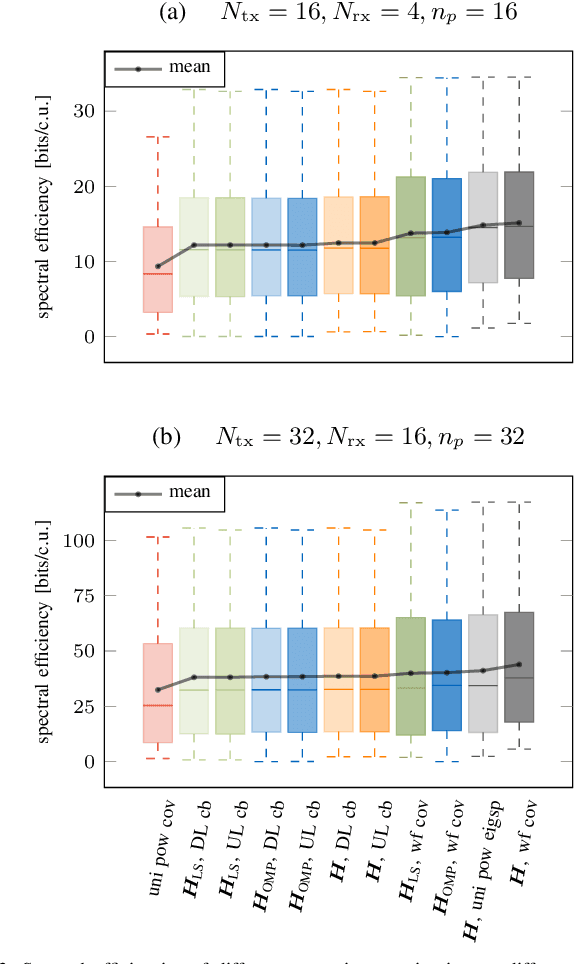
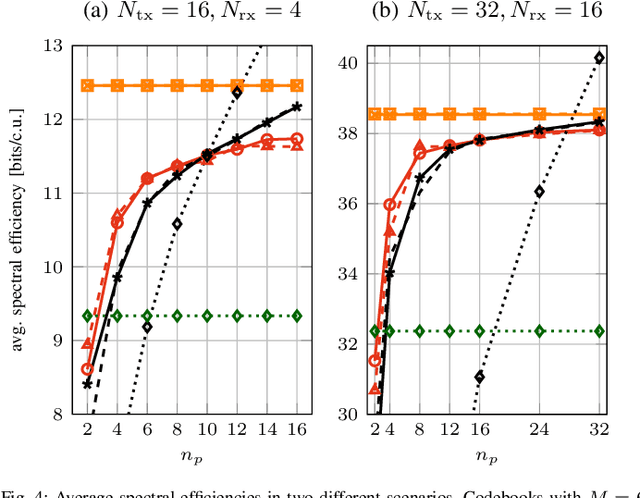
In this work, we propose a joint adaptive codebook construction and feedback generation scheme in frequency division duplex (FDD) systems. Both unsupervised and supervised deep learning techniques are used for this purpose. Based on a recently discovered equivalence of uplink (UL) and downlink (DL) channel state information (CSI) in terms of neural network learning, the codebook and associated deep encoder for feedback signaling is based on UL data only. Subsequently, the feedback encoder can be offloaded to the mobile terminals (MTs) to generate channel feedback there as efficiently as possible, without any training effort at the terminals or corresponding transfer of training and codebook data. Numerical simulations demonstrate the promising performance of the proposed method.