An Asymptotically Optimal Approximation of the Conditional Mean Channel Estimator based on Gaussian Mixture Models

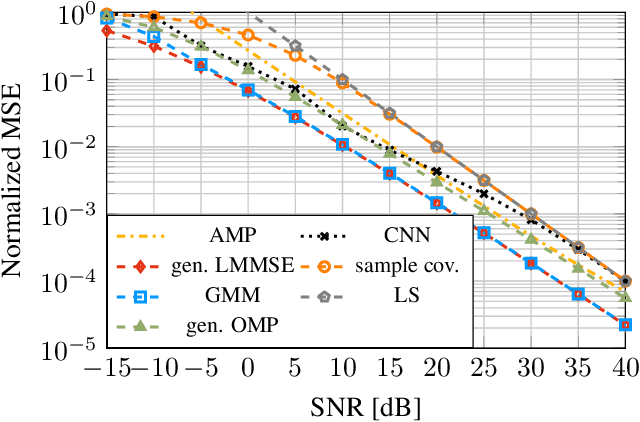
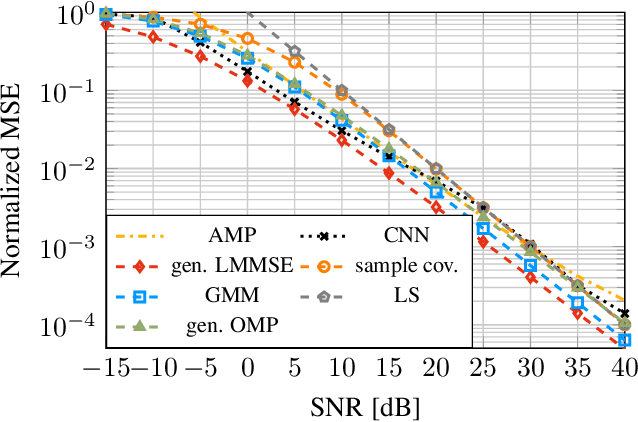
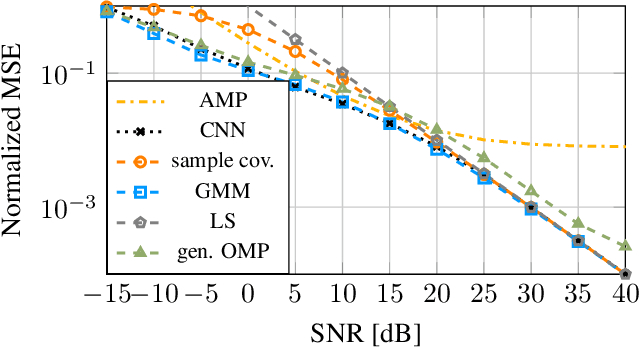
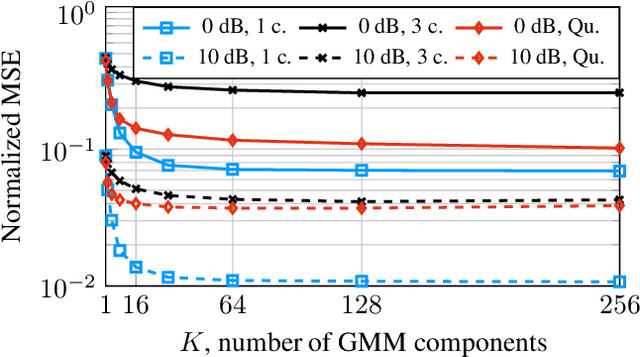
This paper investigates a channel estimator based on Gaussian mixture models (GMMs) in the context of linear inverse problems with additive Gaussian noise. We fit a GMM to given channel samples to obtain an analytic probability density function (PDF) which approximates the true channel PDF. Then, a conditional mean estimator (CME) corresponding to this approximating PDF is computed in closed form and used as an approximation of the optimal CME based on the true channel PDF. This optimal CME cannot be calculated analytically because the true channel PDF is generally unknown. We present mild conditions which allow us to prove the convergence of the GMM-based CME to the optimal CME as the number of GMM components is increased. Additionally, we investigate the estimator's computational complexity and present simplifications based on common model-based insights. Further, we study the estimator's behavior in numerical experiments including multiple-input multiple-output (MIMO) and wideband systems.