Channel Estimation based on Gaussian Mixture Models with Structured Covariances

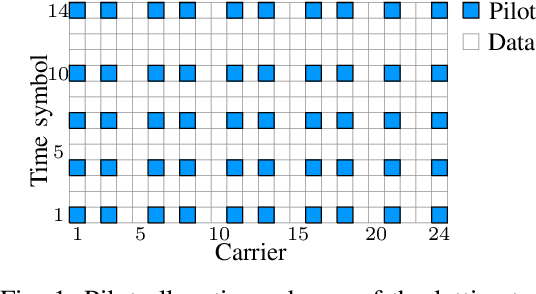
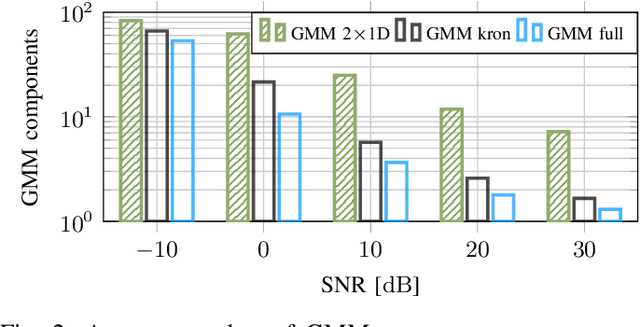
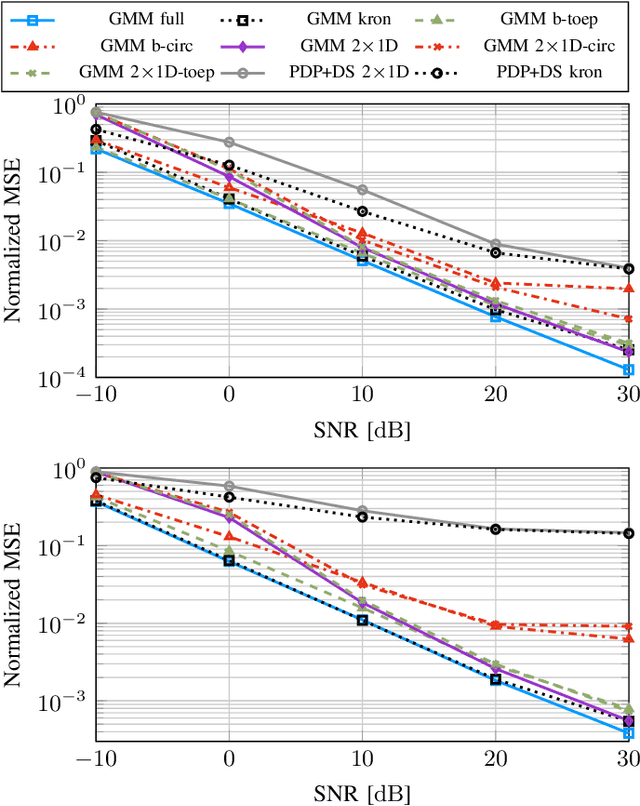
In this work, we propose variations of a Gaussian mixture model (GMM) based channel estimator that was recently proven to be asymptotically optimal in the minimum mean square error (MMSE) sense. We account for the need of low computational complexity in the online estimation and low cost for training and storage in practical applications. To this end, we discuss modifications of the underlying expectation-maximization (EM) algorithm, which is needed to fit the parameters of the GMM, to allow for structurally constrained covariances. Further, we investigate splitting the 2D time and frequency estimation problem in wideband systems into cascaded 1D estimations with the help of the GMM. The proposed cascaded GMM approach drastically reduces the complexity and memory requirements. We observe that due to the training on realistic channel data, the proposed GMM estimators seem to inherently perform a trade-off between saving complexity/parameters and estimation performance. We compare these low-complexity approaches to a practical and low cost method that relies on the power delay profile (PDP) and the Doppler spectrum (DS). We argue that, with the training on scenario-specific data from the environment, these practical baselines are outperformed by far with equal estimation complexity.