Evaluating the Stability of Deep Learning Latent Feature Spaces

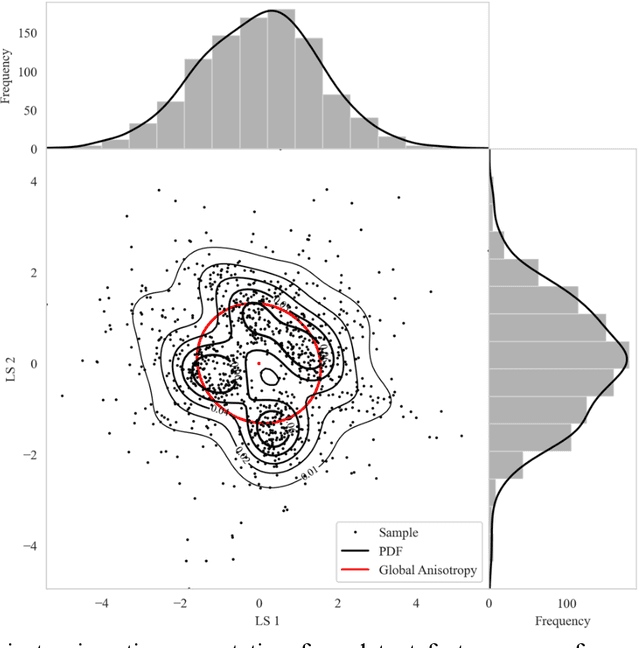
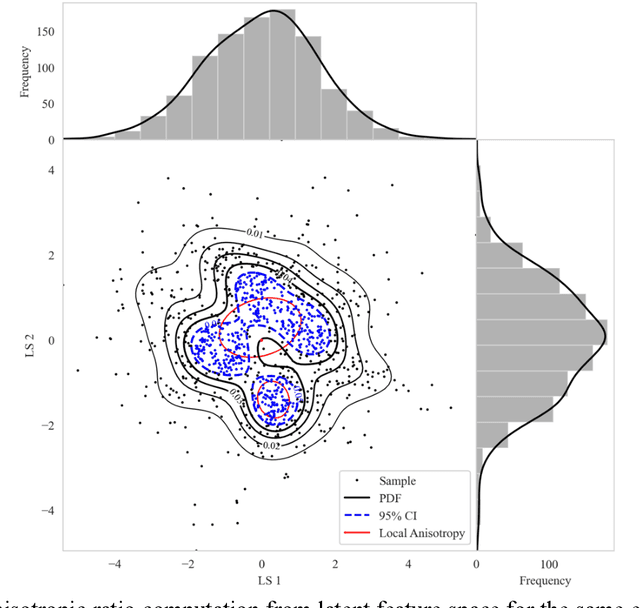
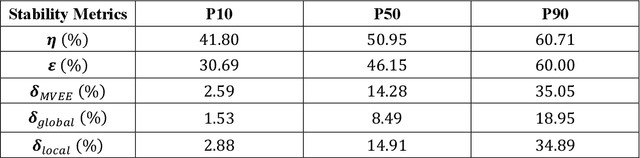
High-dimensional datasets present substantial challenges in statistical modeling across various disciplines, necessitating effective dimensionality reduction methods. Deep learning approaches, notable for their capacity to distill essential features from complex data, facilitate modeling, visualization, and compression through reduced dimensionality latent feature spaces, have wide applications from bioinformatics to earth sciences. This study introduces a novel workflow to evaluate the stability of these latent spaces, ensuring consistency and reliability in subsequent analyses. Stability, defined as the invariance of latent spaces to minor data, training realizations, and parameter perturbations, is crucial yet often overlooked. Our proposed methodology delineates three stability types, sample, structural, and inferential, within latent spaces, and introduces a suite of metrics for comprehensive evaluation. We implement this workflow across 500 autoencoder realizations and three datasets, encompassing both synthetic and real-world scenarios to explain latent space dynamics. Employing k-means clustering and the modified Jonker-Volgenant algorithm for class alignment, alongside anisotropy metrics and convex hull analysis, we introduce adjusted stress and Jaccard dissimilarity as novel stability indicators. Our findings highlight inherent instabilities in latent feature spaces and demonstrate the workflow's efficacy in quantifying and interpreting these instabilities. This work advances the understanding of latent feature spaces, promoting improved model interpretability and quality control for more informed decision-making for diverse analytical workflows that leverage deep learning.

Rigid Transformations for Stabilized Lower Dimensional Space to Support Subsurface Uncertainty Quantification and Interpretation

Subsurface datasets inherently possess big data characteristics such as vast volume, diverse features, and high sampling speeds, further compounded by the curse of dimensionality from various physical, engineering, and geological inputs. Among the existing dimensionality reduction (DR) methods, nonlinear dimensionality reduction (NDR) methods, especially Metric-multidimensional scaling (MDS), are preferred for subsurface datasets due to their inherent complexity. While MDS retains intrinsic data structure and quantifies uncertainty, its limitations include unstabilized unique solutions invariant to Euclidean transformations and an absence of out-of-sample points (OOSP) extension. To enhance subsurface inferential and machine learning workflows, datasets must be transformed into stable, reduced-dimension representations that accommodate OOSP. Our solution employs rigid transformations for a stabilized Euclidean invariant representation for LDS. By computing an MDS input dissimilarity matrix, and applying rigid transformations on multiple realizations, we ensure transformation invariance and integrate OOSP. This process leverages a convex hull algorithm and incorporates loss function and normalized stress for distortion quantification. We validate our approach with synthetic data, varying distance metrics, and real-world wells from the Duvernay Formation. Results confirm our method's efficacy in achieving consistent LDS representations. Furthermore, our proposed "stress ratio" (SR) metric provides insight into uncertainty, beneficial for model adjustments and inferential analysis. Consequently, our workflow promises enhanced repeatability and comparability in NDR for subsurface energy resource engineering and associated big data workflows.

Mitigation of Spatial Nonstationarity with Vision Transformers

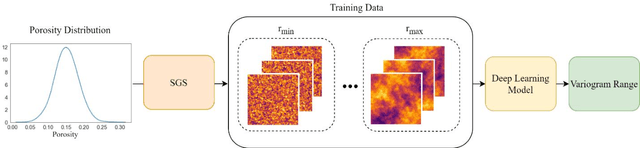
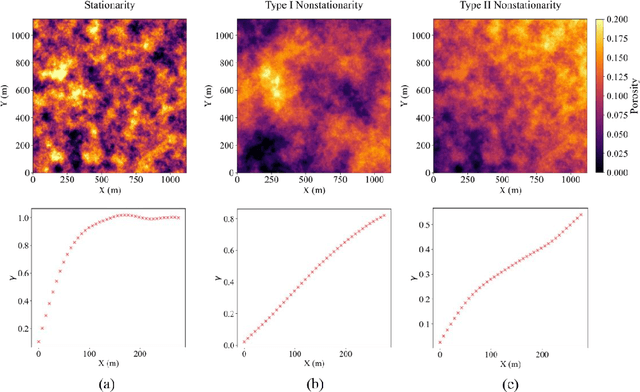
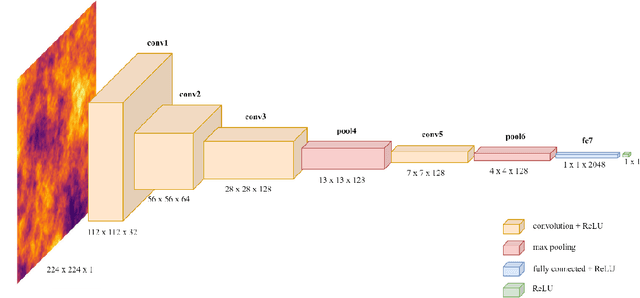
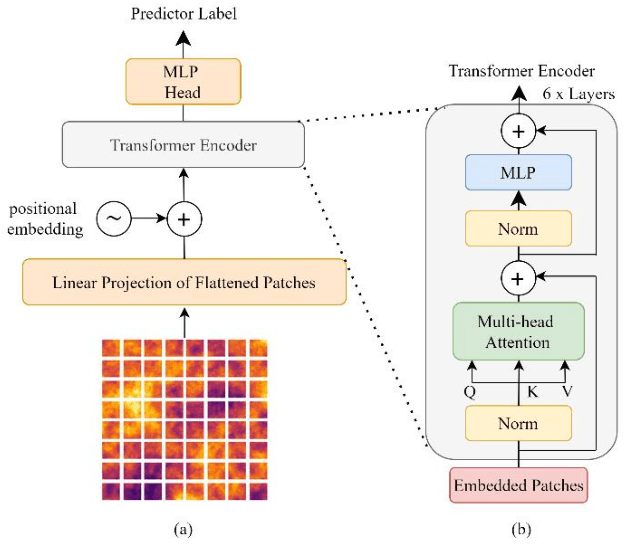
Spatial nonstationarity, the location variance of features' statistical distributions, is ubiquitous in many natural settings. For example, in geological reservoirs rock matrix porosity varies vertically due to geomechanical compaction trends, in mineral deposits grades vary due to sedimentation and concentration processes, in hydrology rainfall varies due to the atmosphere and topography interactions, and in metallurgy crystalline structures vary due to differential cooling. Conventional geostatistical modeling workflows rely on the assumption of stationarity to be able to model spatial features for the geostatistical inference. Nevertheless, this is often not a realistic assumption when dealing with nonstationary spatial data and this has motivated a variety of nonstationary spatial modeling workflows such as trend and residual decomposition, cosimulation with secondary features, and spatial segmentation and independent modeling over stationary subdomains. The advent of deep learning technologies has enabled new workflows for modeling spatial relationships. However, there is a paucity of demonstrated best practice and general guidance on mitigation of spatial nonstationarity with deep learning in the geospatial context. We demonstrate the impact of two common types of geostatistical spatial nonstationarity on deep learning model prediction performance and propose the mitigation of such impacts using self-attention (vision transformer) models. We demonstrate the utility of vision transformers for the mitigation of nonstationarity with relative errors as low as 10%, exceeding the performance of alternative deep learning methods such as convolutional neural networks. We establish best practice by demonstrating the ability of self-attention networks for modeling large-scale spatial relationships in the presence of commonly observed geospatial nonstationarity.

Physics-Informed Graph Neural Network for Spatial-temporal Production Forecasting

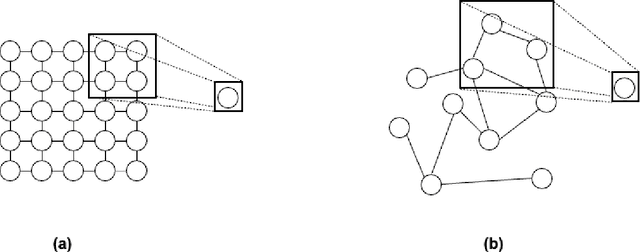
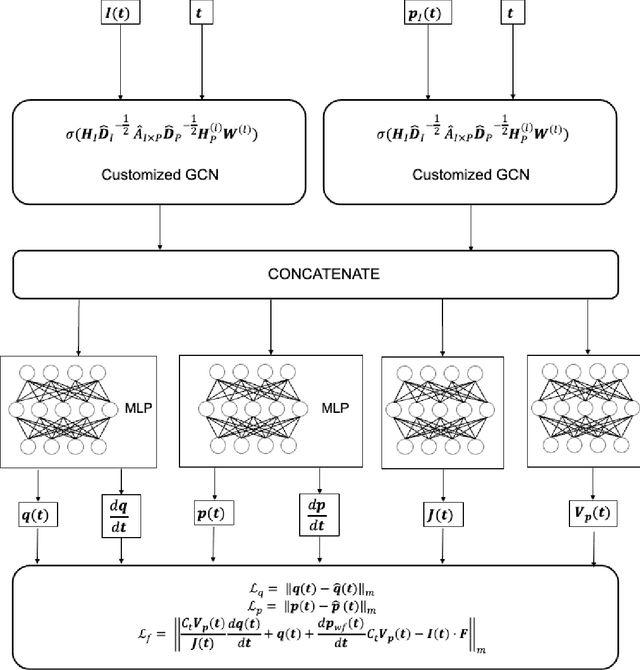
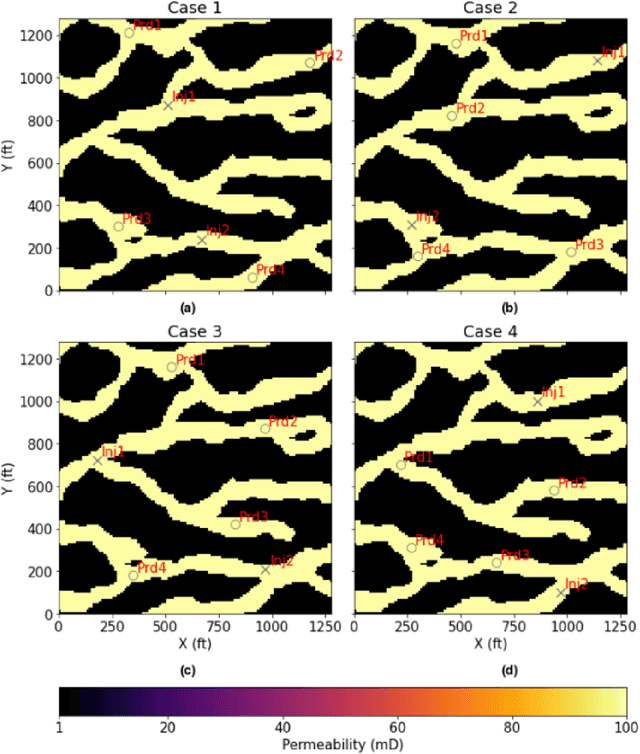
Production forecast based on historical data provides essential value for developing hydrocarbon resources. Classic history matching workflow is often computationally intense and geometry-dependent. Analytical data-driven models like decline curve analysis (DCA) and capacitance resistance models (CRM) provide a grid-free solution with a relatively simple model capable of integrating some degree of physics constraints. However, the analytical solution may ignore subsurface geometries and is appropriate only for specific flow regimes and otherwise may violate physics conditions resulting in degraded model prediction accuracy. Machine learning-based predictive model for time series provides non-parametric, assumption-free solutions for production forecasting, but are prone to model overfit due to training data sparsity; therefore may be accurate over short prediction time intervals. We propose a grid-free, physics-informed graph neural network (PI-GNN) for production forecasting. A customized graph convolution layer aggregates neighborhood information from historical data and has the flexibility to integrate domain expertise into the data-driven model. The proposed method relaxes the dependence on close-form solutions like CRM and honors the given physics-based constraints. Our proposed method is robust, with improved performance and model interpretability relative to the conventional CRM and GNN baseline without physics constraints.

A recommender system for automatic picking of subsurface formation tops

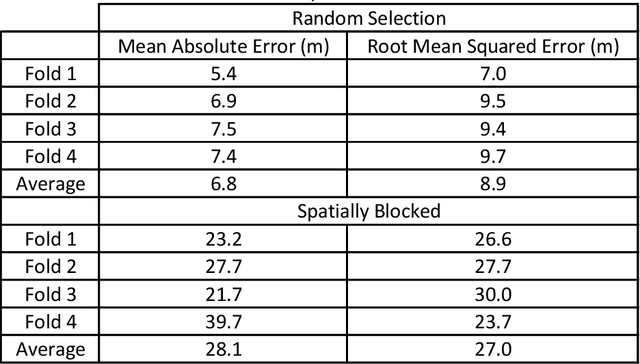
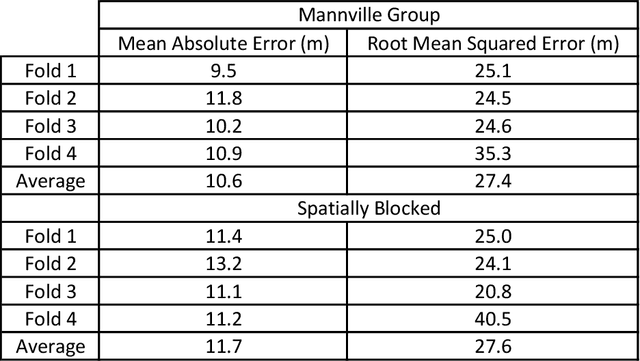
Geoscience domain experts traditionally correlate formation tops in the subsurface using geophysical well logs (known as well-log correlation) by-hand. Based on individual well log interpretation and well-to-well comparisons, these correlations are done in the context of depositional models within a stratigraphic framework. Recently, many researchers have focused on automatic well-log correlation using a variety of warping algorithms that measure well similarity, and both unsupervised and supervised machine learning methods that assign categorical labels based on known tops in many other wells. These methods require a standardized suite of digital well logs (i.e. gamma ray logs for every well) along with the depth to the top of the formations, which might not be available in many cases. Herein, we propose a method that does not use geophysical well logs for correlation, but rather uses already picked tops in multiple wells to recommend the depth to the remaining unpicked tops in the wells. This recommender system calculates the depth to all formation tops in all the wells for two different datasets in two different basins. The Teapot Dome dataset is composed of lithostratigraphic formation tops, and the Mannville Group dataset is composed of sequence-stratigraphic (representing multiple lithologic groups within a stratigraphic unit) formation tops. For the demonstration, mean absolute error and root mean squared error of four-fold cross-validation compares the recommender system predictions to the ground truth human interpretations. The recommender system is competitive and often outperforms state of the art spline interpolation methods. Lastly, increasing the size of the training dataset decreases the prediction error, and that variance in error decreases with increasing formation tops picked in each formation and well for the lithostratigraphic top picks.

Machine learning-based porosity estimation from spectral decomposed seismic data

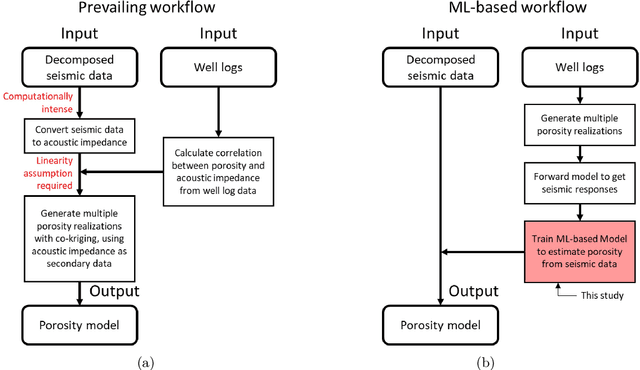
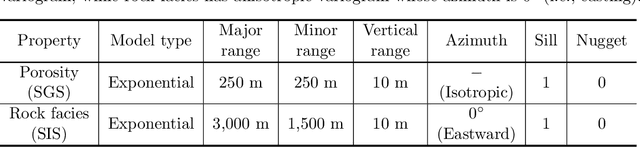
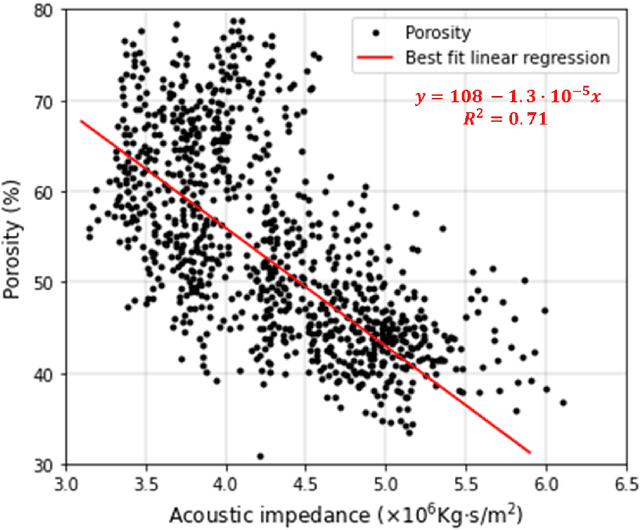
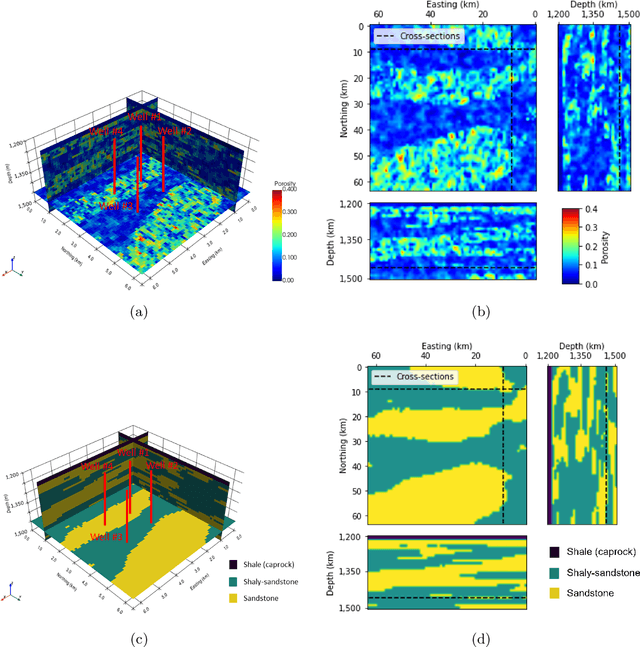
Estimating porosity models via seismic data is challenging due to the signal noise and insufficient resolution of seismic data. Although impedance inversion is often used by combining with well logs, several hurdles remain to retrieve sub-seismic scale porosity. As an alternative, we propose a machine learning-based workflow to convert seismic data to porosity models. A ResUNet++ based workflow is designed to take three seismic data in different frequencies (i.e., decomposed seismic data) and estimate their corresponding porosity model. The workflow is successfully demonstrated in the 3D channelized reservoir to estimate the porosity model with more than 0.9 in R2 score for training and validating data. Moreover, the application is extended for a stress test by adding signal noise to the seismic data, and the workflow results show a robust estimation even with 5\% of noise. Another two ResUNet++ are trained to take either the lowest or highest resolution seismic data only to estimate the porosity model, but they show under- and over-fitting results, supporting the importance of using decomposed seismic data in porosity estimation.

Automatic Feature Highlighting in Noisy RES Data With CycleGAN

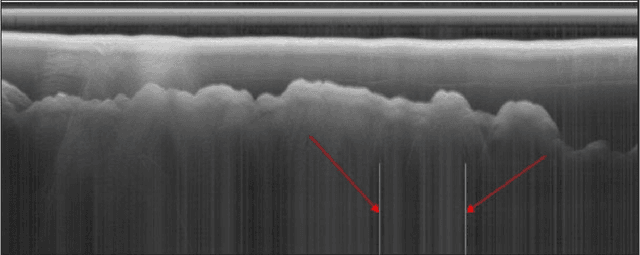
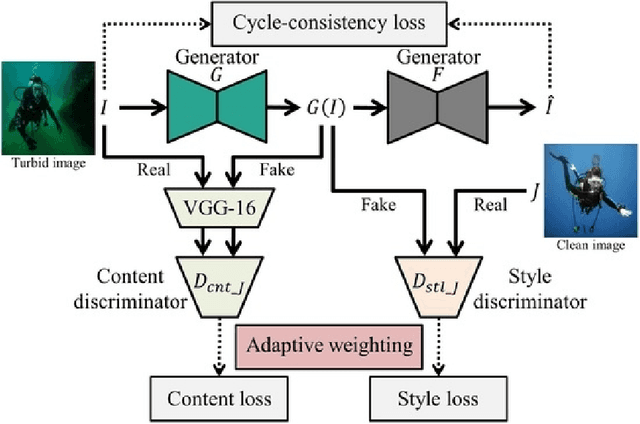
Radio echo sounding (RES) is a common technique used in subsurface glacial imaging, which provides insight into the underlying rock and ice. However, systematic noise is introduced into the data during collection, complicating interpretation of the results. Researchers most often use a combination of manual interpretation and filtering techniques to denoise data; however, these processes are time intensive and inconsistent. Fully Convolutional Networks have been proposed as an automated alternative to identify layer boundaries in radargrams. However, they require high-quality manually processed training data and struggle to interpolate data in noisy samples (Varshney et al. 2020). Herein, the authors propose a GAN based model to interpolate layer boundaries through noise and highlight layers in two-dimensional glacial RES data. In real-world noisy images, filtering often results in loss of data such that interpolating layer boundaries is nearly impossible. Furthermore, traditional machine learning approaches are not suited to this task because of the lack of paired data, so we employ an unpaired image-to-image translation model. For this model, we create a synthetic dataset to represent the domain of images with clear, highlighted layers and use an existing real-world RES dataset as our noisy domain. We implement a CycleGAN trained on these two domains to highlight layers in noisy images that can interpolate effectively without significant loss of structure or fidelity. Though the current implementation is not a perfect solution, the model clearly highlights layers in noisy data and allows researchers to determine layer size and position without mathematical filtering, manual processing, or ground-truth images for training. This is significant because clean images generated by our model enable subsurface researchers to determine glacial layer thickness more efficiently.

Optimal Placement of Public Electric Vehicle Charging Stations Using Deep Reinforcement Learning

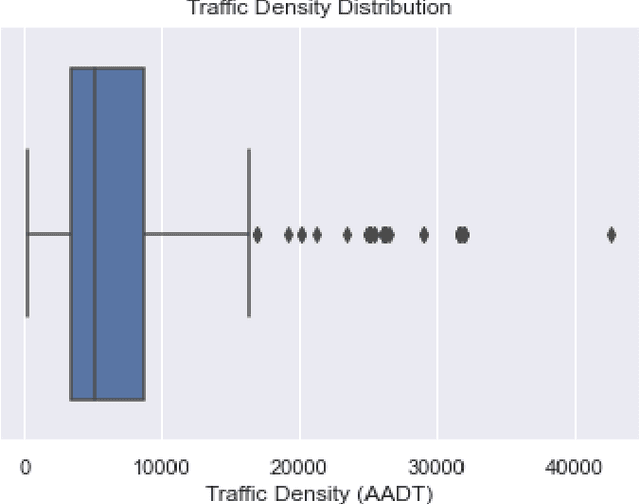
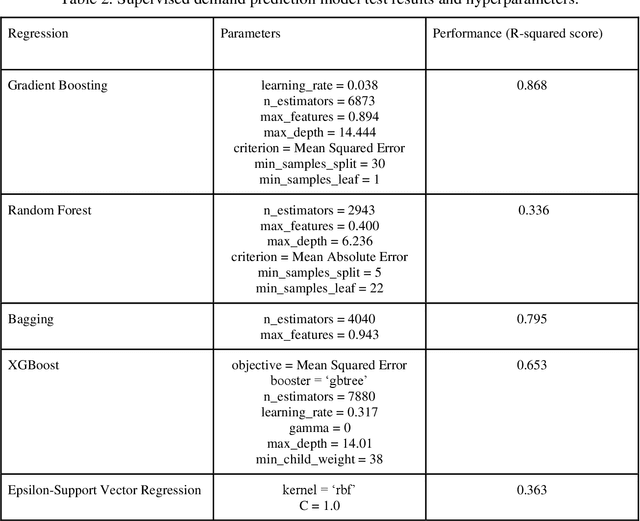
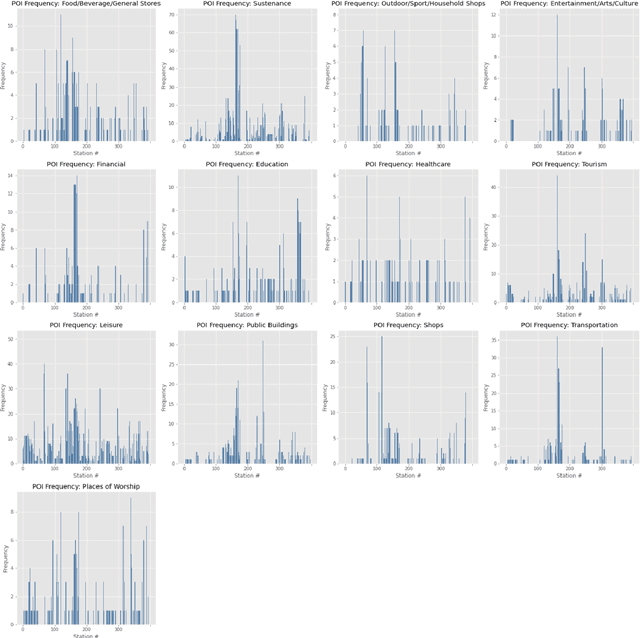
The placement of charging stations in areas with developing charging infrastructure is a critical component of the future success of electric vehicles (EVs). In Albany County in New York, the expected rise in the EV population requires additional charging stations to maintain a sufficient level of efficiency across the charging infrastructure. A novel application of Reinforcement Learning (RL) is able to find optimal locations for new charging stations given the predicted charging demand and current charging locations. The most important factors that influence charging demand prediction include the conterminous traffic density, EV registrations, and proximity to certain types of public buildings. The proposed RL framework can be refined and applied to cities across the world to optimize charging station placement.

Modeling nanoconfinement effects using active learning

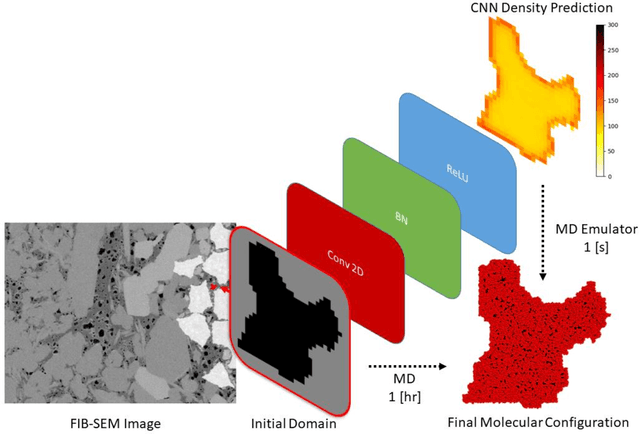
Predicting the spatial configuration of gas molecules in nanopores of shale formations is crucial for fluid flow forecasting and hydrocarbon reserves estimation. The key challenge in these tight formations is that the majority of the pore sizes are less than 50 nm. At this scale, the fluid properties are affected by nanoconfinement effects due to the increased fluid-solid interactions. For instance, gas adsorption to the pore walls could account for up to 85% of the total hydrocarbon volume in a tight reservoir. Although there are analytical solutions that describe this phenomenon for simple geometries, they are not suitable for describing realistic pores, where surface roughness and geometric anisotropy play important roles. To describe these, molecular dynamics (MD) simulations are used since they consider fluid-solid and fluid-fluid interactions at the molecular level. However, MD simulations are computationally expensive, and are not able to simulate scales larger than a few connected nanopores. We present a method for building and training physics-based deep learning surrogate models to carry out fast and accurate predictions of molecular configurations of gas inside nanopores. Since training deep learning models requires extensive databases that are computationally expensive to create, we employ active learning (AL). AL reduces the overhead of creating comprehensive sets of high-fidelity data by determining where the model uncertainty is greatest, and running simulations on the fly to minimize it. The proposed workflow enables nanoconfinement effects to be rigorously considered at the mesoscale where complex connected sets of nanopores control key applications such as hydrocarbon recovery and CO2 sequestration.