Machine Learning-Based Completions Sequencing for Well Performance Optimization

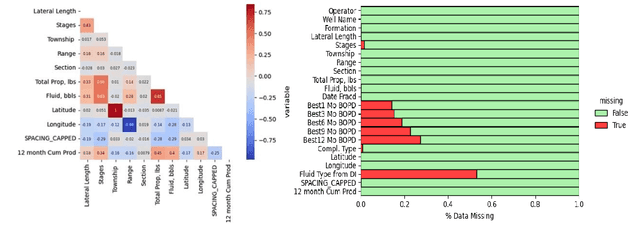
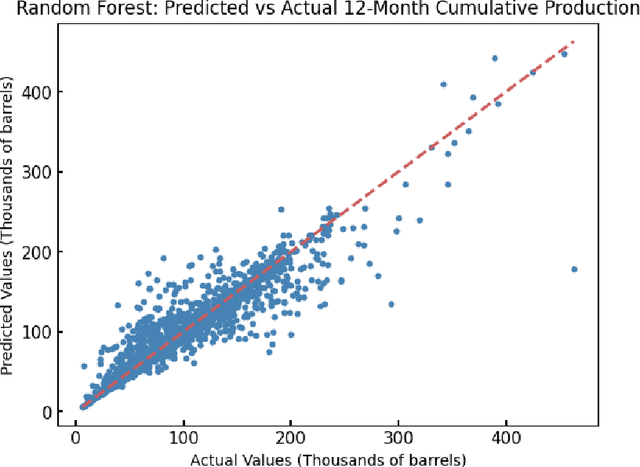
Establishing accurate field development parameters to optimize long-term oil production takes time and effort due to the complexity of oil well development, and the uncertainty in estimating long-term well production. Traditionally, oil and gas companies use simulation software that are inherently computationally expensive to forecast production. Thus, machine learning approaches are recently utilized in literature as an efficient alternative to optimize well developments by enhancing completion conditions. The primary goal of this project is to develop effective machine-learning models that can integrate the effects of multidimensional predictive variables (i.e., completion conditions) to predict 12-Month Cumulative Production accurately. Three predictive regression machine learning models are implemented for predicting 12-month cumulative oil production: Random Forest, Gradient Boosting, and Long Short-Term Memory Models. All three models yielded cumulative production predictions with root mean squared error (RMSE ) values ranging from 7.35 to 20.01 thousand barrels of oil. Although we hypothesized that all models would yield accurate predictions, the results indicated a crucial need for further refinement to create reliable and rational predictive tools in the subsurface. While this study did not produce optimal models for completion sequencing to maximize long-term production, we established that machine learning models alone are not self-sufficient for problems of this nature. Hence, there is potential for significant improvement, including comprehensive feature engineering, and a recommendation of exploring the use of hybrid or surrogate models (i.e., coupling physics reduced models and machine learning models), to ascertain significant contribution to the progress of completion sequencing workflows.

Evaluating the Stability of Deep Learning Latent Feature Spaces

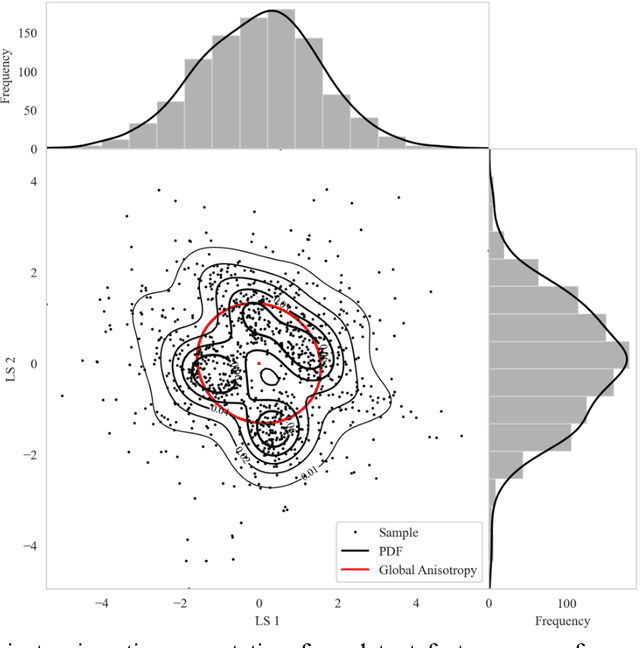
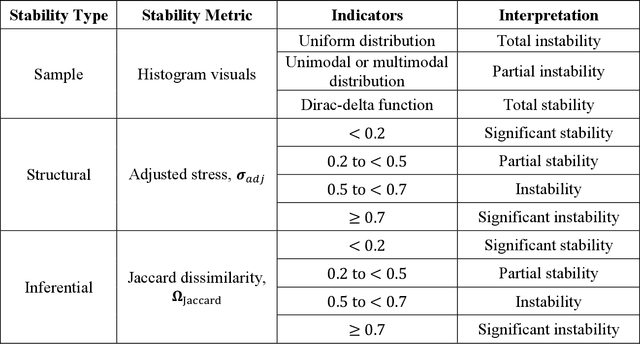
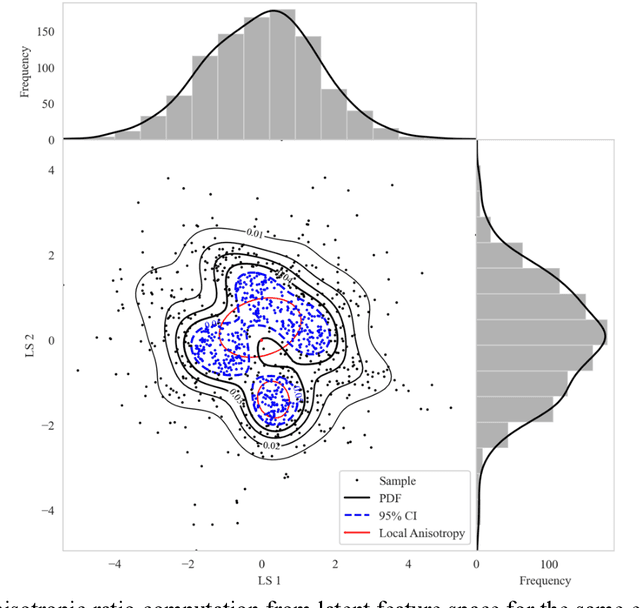
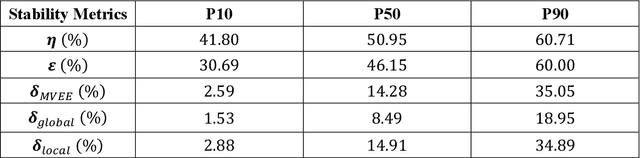
High-dimensional datasets present substantial challenges in statistical modeling across various disciplines, necessitating effective dimensionality reduction methods. Deep learning approaches, notable for their capacity to distill essential features from complex data, facilitate modeling, visualization, and compression through reduced dimensionality latent feature spaces, have wide applications from bioinformatics to earth sciences. This study introduces a novel workflow to evaluate the stability of these latent spaces, ensuring consistency and reliability in subsequent analyses. Stability, defined as the invariance of latent spaces to minor data, training realizations, and parameter perturbations, is crucial yet often overlooked. Our proposed methodology delineates three stability types, sample, structural, and inferential, within latent spaces, and introduces a suite of metrics for comprehensive evaluation. We implement this workflow across 500 autoencoder realizations and three datasets, encompassing both synthetic and real-world scenarios to explain latent space dynamics. Employing k-means clustering and the modified Jonker-Volgenant algorithm for class alignment, alongside anisotropy metrics and convex hull analysis, we introduce adjusted stress and Jaccard dissimilarity as novel stability indicators. Our findings highlight inherent instabilities in latent feature spaces and demonstrate the workflow's efficacy in quantifying and interpreting these instabilities. This work advances the understanding of latent feature spaces, promoting improved model interpretability and quality control for more informed decision-making for diverse analytical workflows that leverage deep learning.

Rigid Transformations for Stabilized Lower Dimensional Space to Support Subsurface Uncertainty Quantification and Interpretation

Subsurface datasets inherently possess big data characteristics such as vast volume, diverse features, and high sampling speeds, further compounded by the curse of dimensionality from various physical, engineering, and geological inputs. Among the existing dimensionality reduction (DR) methods, nonlinear dimensionality reduction (NDR) methods, especially Metric-multidimensional scaling (MDS), are preferred for subsurface datasets due to their inherent complexity. While MDS retains intrinsic data structure and quantifies uncertainty, its limitations include unstabilized unique solutions invariant to Euclidean transformations and an absence of out-of-sample points (OOSP) extension. To enhance subsurface inferential and machine learning workflows, datasets must be transformed into stable, reduced-dimension representations that accommodate OOSP. Our solution employs rigid transformations for a stabilized Euclidean invariant representation for LDS. By computing an MDS input dissimilarity matrix, and applying rigid transformations on multiple realizations, we ensure transformation invariance and integrate OOSP. This process leverages a convex hull algorithm and incorporates loss function and normalized stress for distortion quantification. We validate our approach with synthetic data, varying distance metrics, and real-world wells from the Duvernay Formation. Results confirm our method's efficacy in achieving consistent LDS representations. Furthermore, our proposed "stress ratio" (SR) metric provides insight into uncertainty, beneficial for model adjustments and inferential analysis. Consequently, our workflow promises enhanced repeatability and comparability in NDR for subsurface energy resource engineering and associated big data workflows.