Michael G. Forbes
Guiding Reinforcement Learning with Incomplete System Dynamics
Oct 24, 2024Abstract:Model-free reinforcement learning (RL) is inherently a reactive method, operating under the assumption that it starts with no prior knowledge of the system and entirely depends on trial-and-error for learning. This approach faces several challenges, such as poor sample efficiency, generalization, and the need for well-designed reward functions to guide learning effectively. On the other hand, controllers based on complete system dynamics do not require data. This paper addresses the intermediate situation where there is not enough model information for complete controller design, but there is enough to suggest that a model-free approach is not the best approach either. By carefully decoupling known and unknown information about the system dynamics, we obtain an embedded controller guided by our partial model and thus improve the learning efficiency of an RL-enhanced approach. A modular design allows us to deploy mainstream RL algorithms to refine the policy. Simulation results show that our method significantly improves sample efficiency compared with standard RL methods on continuous control tasks, and also offers enhanced performance over traditional control approaches. Experiments on a real ground vehicle also validate the performance of our method, including generalization and robustness.
Stabilizing reinforcement learning control: A modular framework for optimizing over all stable behavior
Oct 21, 2023



Abstract:We propose a framework for the design of feedback controllers that combines the optimization-driven and model-free advantages of deep reinforcement learning with the stability guarantees provided by using the Youla-Kucera parameterization to define the search domain. Recent advances in behavioral systems allow us to construct a data-driven internal model; this enables an alternative realization of the Youla-Kucera parameterization based entirely on input-output exploration data. Perhaps of independent interest, we formulate and analyze the stability of such data-driven models in the presence of noise. The Youla-Kucera approach requires a stable "parameter" for controller design. For the training of reinforcement learning agents, the set of all stable linear operators is given explicitly through a matrix factorization approach. Moreover, a nonlinear extension is given using a neural network to express a parameterized set of stable operators, which enables seamless integration with standard deep learning libraries. Finally, we show how these ideas can also be applied to tune fixed-structure controllers.
Reinforcement Learning with Partial Parametric Model Knowledge
Apr 26, 2023Abstract:We adapt reinforcement learning (RL) methods for continuous control to bridge the gap between complete ignorance and perfect knowledge of the environment. Our method, Partial Knowledge Least Squares Policy Iteration (PLSPI), takes inspiration from both model-free RL and model-based control. It uses incomplete information from a partial model and retains RL's data-driven adaption towards optimal performance. The linear quadratic regulator provides a case study; numerical experiments demonstrate the effectiveness and resulting benefits of the proposed method.
A modular framework for stabilizing deep reinforcement learning control
Apr 07, 2023Abstract:We propose a framework for the design of feedback controllers that combines the optimization-driven and model-free advantages of deep reinforcement learning with the stability guarantees provided by using the Youla-Kucera parameterization to define the search domain. Recent advances in behavioral systems allow us to construct a data-driven internal model; this enables an alternative realization of the Youla-Kucera parameterization based entirely on input-output exploration data. Using a neural network to express a parameterized set of nonlinear stable operators enables seamless integration with standard deep learning libraries. We demonstrate the approach on a realistic simulation of a two-tank system.
Meta-Reinforcement Learning for Adaptive Control of Second Order Systems
Sep 19, 2022
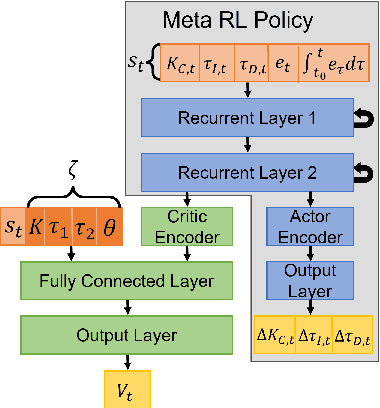
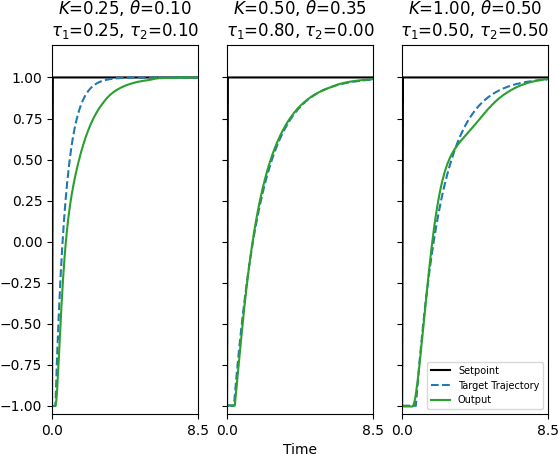
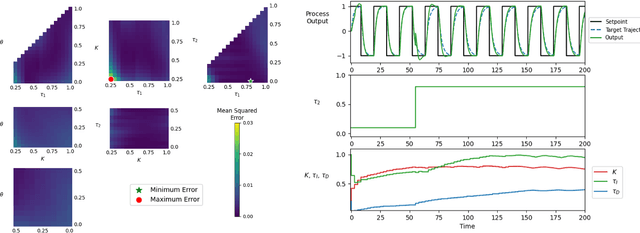
Abstract:Meta-learning is a branch of machine learning which aims to synthesize data from a distribution of related tasks to efficiently solve new ones. In process control, many systems have similar and well-understood dynamics, which suggests it is feasible to create a generalizable controller through meta-learning. In this work, we formulate a meta reinforcement learning (meta-RL) control strategy that takes advantage of known, offline information for training, such as a model structure. The meta-RL agent is trained over a distribution of model parameters, rather than a single model, enabling the agent to automatically adapt to changes in the process dynamics while maintaining performance. A key design element is the ability to leverage model-based information offline during training, while maintaining a model-free policy structure for interacting with new environments. Our previous work has demonstrated how this approach can be applied to the industrially-relevant problem of tuning proportional-integral controllers to control first order processes. In this work, we briefly reintroduce our methodology and demonstrate how it can be extended to proportional-integral-derivative controllers and second order systems.
Meta Reinforcement Learning for Adaptive Control: An Offline Approach
Mar 17, 2022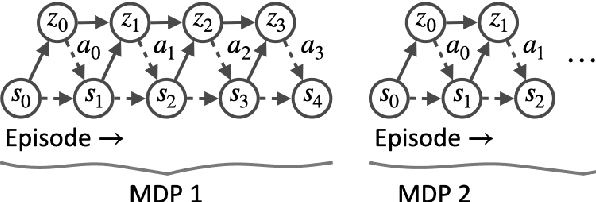
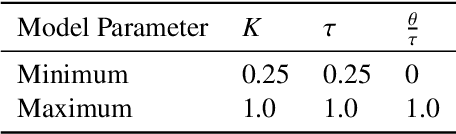
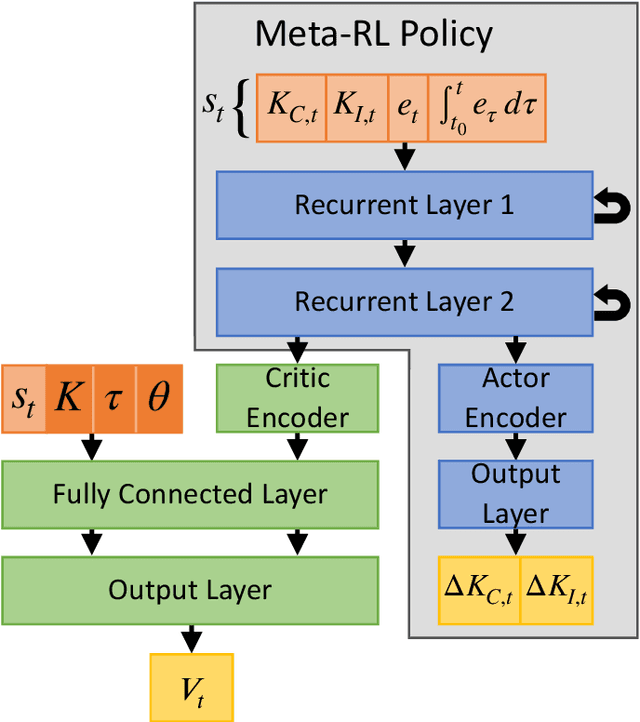
Abstract:Meta-learning is a branch of machine learning which trains neural network models to synthesize a wide variety of data in order to rapidly solve new problems. In process control, many systems have similar and well-understood dynamics, which suggests it is feasible to create a generalizable controller through meta-learning. In this work, we formulate a meta reinforcement learning (meta-RL) control strategy that takes advantage of known, offline information for training, such as the system gain or time constant, yet efficiently controls novel systems in a completely model-free fashion. Our meta-RL agent has a recurrent structure that accumulates "context" for its current dynamics through a hidden state variable. This end-to-end architecture enables the agent to automatically adapt to changes in the process dynamics. Moreover, the same agent can be deployed on systems with previously unseen nonlinearities and timescales. In tests reported here, the meta-RL agent was trained entirely offline, yet produced excellent results in novel settings. A key design element is the ability to leverage model-based information offline during training, while maintaining a model-free policy structure for interacting with novel environments. To illustrate the approach, we take the actions proposed by the meta-RL agent to be changes to gains of a proportional-integral controller, resulting in a generalized, adaptive, closed-loop tuning strategy. Meta-learning is a promising approach for constructing sample-efficient intelligent controllers.
Deep Reinforcement Learning with Shallow Controllers: An Experimental Application to PID Tuning
Nov 13, 2021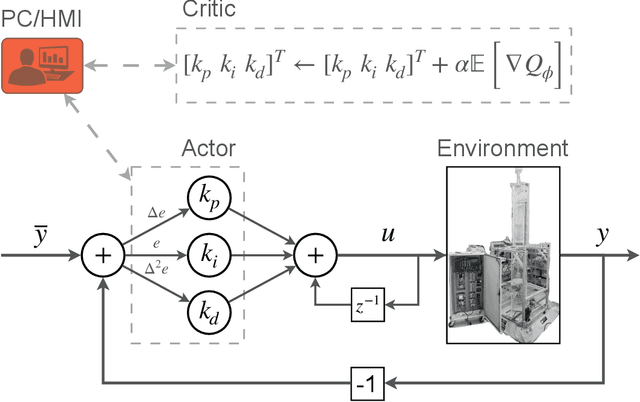


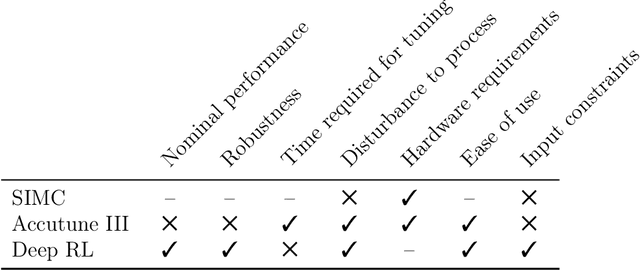
Abstract:Deep reinforcement learning (RL) is an optimization-driven framework for producing control strategies for general dynamical systems without explicit reliance on process models. Good results have been reported in simulation. Here we demonstrate the challenges in implementing a state of the art deep RL algorithm on a real physical system. Aspects include the interplay between software and existing hardware; experiment design and sample efficiency; training subject to input constraints; and interpretability of the algorithm and control law. At the core of our approach is the use of a PID controller as the trainable RL policy. In addition to its simplicity, this approach has several appealing features: No additional hardware needs to be added to the control system, since a PID controller can easily be implemented through a standard programmable logic controller; the control law can easily be initialized in a "safe'' region of the parameter space; and the final product -- a well-tuned PID controller -- has a form that practitioners can reason about and deploy with confidence.
Almost Surely Stable Deep Dynamics
Mar 26, 2021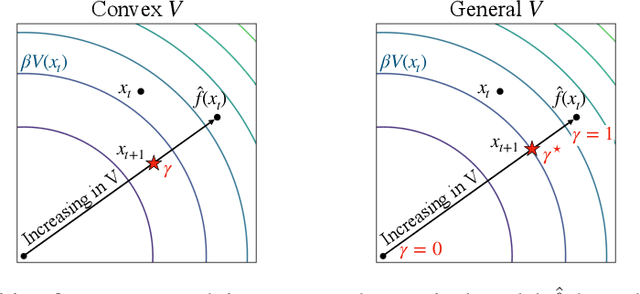
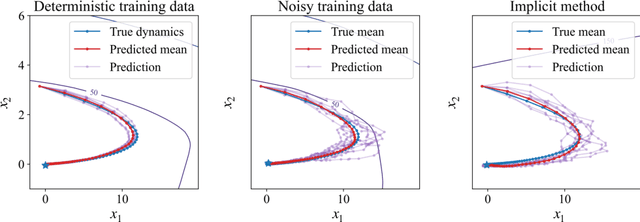
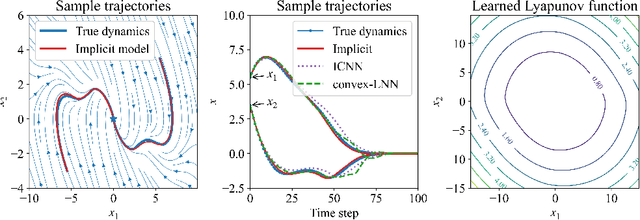
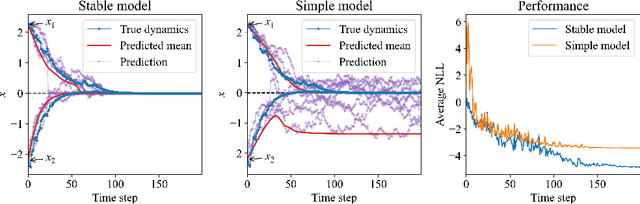
Abstract:We introduce a method for learning provably stable deep neural network based dynamic models from observed data. Specifically, we consider discrete-time stochastic dynamic models, as they are of particular interest in practical applications such as estimation and control. However, these aspects exacerbate the challenge of guaranteeing stability. Our method works by embedding a Lyapunov neural network into the dynamic model, thereby inherently satisfying the stability criterion. To this end, we propose two approaches and apply them in both the deterministic and stochastic settings: one exploits convexity of the Lyapunov function, while the other enforces stability through an implicit output layer. We demonstrate the utility of each approach through numerical examples.
* NeurIPS 2020; Spotlight Paper
A Meta-Reinforcement Learning Approach to Process Control
Mar 25, 2021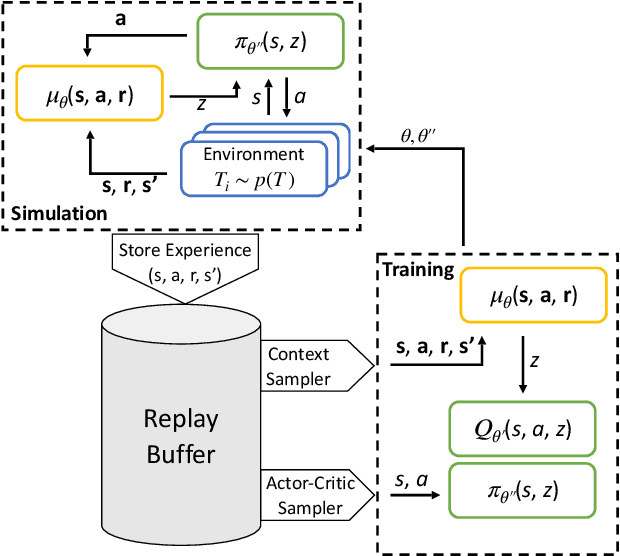
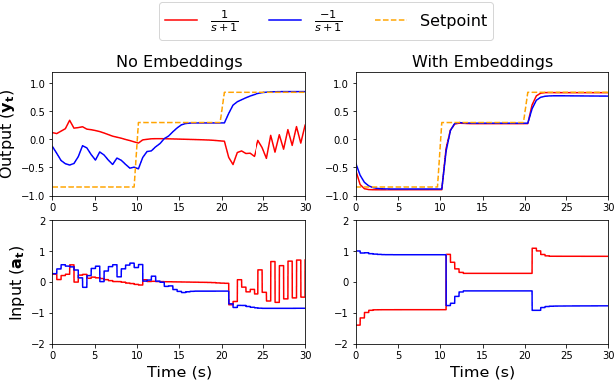

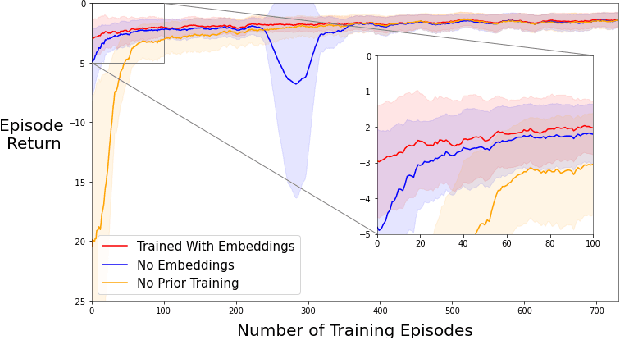
Abstract:Meta-learning is a branch of machine learning which aims to quickly adapt models, such as neural networks, to perform new tasks by learning an underlying structure across related tasks. In essence, models are being trained to learn new tasks effectively rather than master a single task. Meta-learning is appealing for process control applications because the perturbations to a process required to train an AI controller can be costly and unsafe. Additionally, the dynamics and control objectives are similar across many different processes, so it is feasible to create a generalizable controller through meta-learning capable of quickly adapting to different systems. In this work, we construct a deep reinforcement learning (DRL) based controller and meta-train the controller using a latent context variable through a separate embedding neural network. We test our meta-algorithm on its ability to adapt to new process dynamics as well as different control objectives on the same process. In both cases, our meta-learning algorithm adapts very quickly to new tasks, outperforming a regular DRL controller trained from scratch. Meta-learning appears to be a promising approach for constructing more intelligent and sample-efficient controllers.
Optimal PID and Antiwindup Control Design as a Reinforcement Learning Problem
May 10, 2020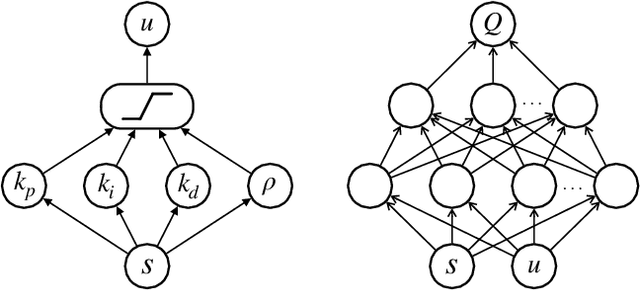


Abstract:Deep reinforcement learning (DRL) has seen several successful applications to process control. Common methods rely on a deep neural network structure to model the controller or process. With increasingly complicated control structures, the closed-loop stability of such methods becomes less clear. In this work, we focus on the interpretability of DRL control methods. In particular, we view linear fixed-structure controllers as shallow neural networks embedded in the actor-critic framework. PID controllers guide our development due to their simplicity and acceptance in industrial practice. We then consider input saturation, leading to a simple nonlinear control structure. In order to effectively operate within the actuator limits we then incorporate a tuning parameter for anti-windup compensation. Finally, the simplicity of the controller allows for straightforward initialization. This makes our method inherently stabilizing, both during and after training, and amenable to known operational PID gains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge