Meta-Reinforcement Learning for Adaptive Control of Second Order Systems
Paper and Code
Sep 19, 2022
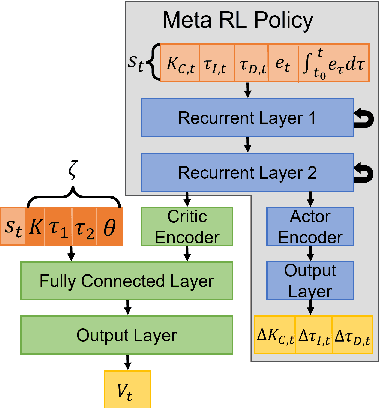
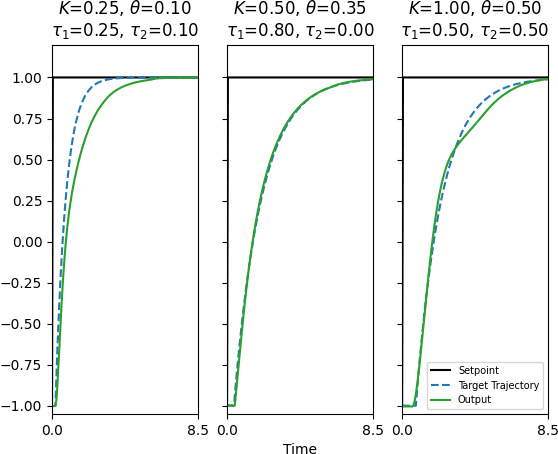
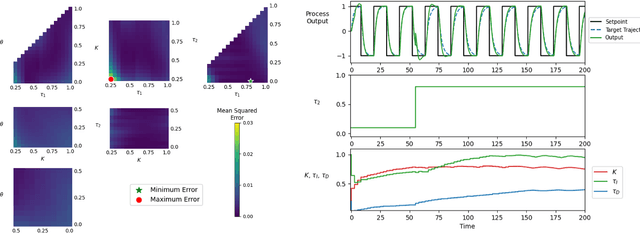
Meta-learning is a branch of machine learning which aims to synthesize data from a distribution of related tasks to efficiently solve new ones. In process control, many systems have similar and well-understood dynamics, which suggests it is feasible to create a generalizable controller through meta-learning. In this work, we formulate a meta reinforcement learning (meta-RL) control strategy that takes advantage of known, offline information for training, such as a model structure. The meta-RL agent is trained over a distribution of model parameters, rather than a single model, enabling the agent to automatically adapt to changes in the process dynamics while maintaining performance. A key design element is the ability to leverage model-based information offline during training, while maintaining a model-free policy structure for interacting with new environments. Our previous work has demonstrated how this approach can be applied to the industrially-relevant problem of tuning proportional-integral controllers to control first order processes. In this work, we briefly reintroduce our methodology and demonstrate how it can be extended to proportional-integral-derivative controllers and second order systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge