Meta-Reinforcement Learning for Adaptive Control of Second Order Systems

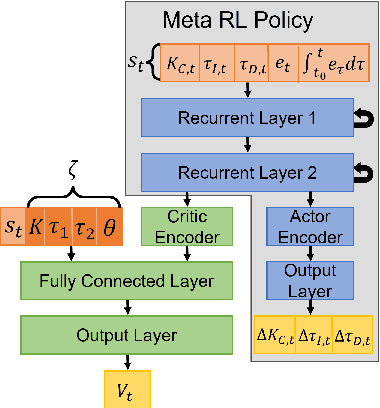
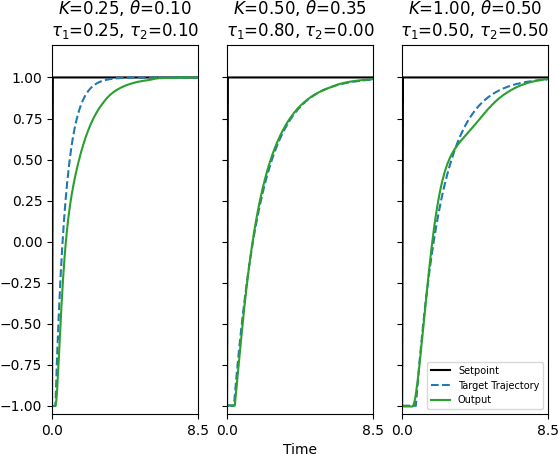
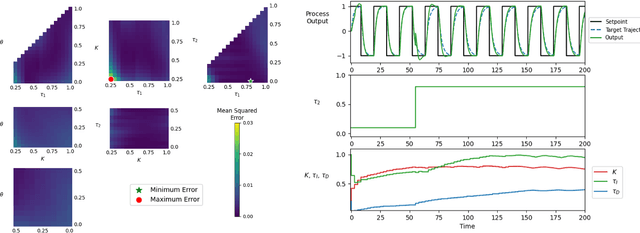
Meta-learning is a branch of machine learning which aims to synthesize data from a distribution of related tasks to efficiently solve new ones. In process control, many systems have similar and well-understood dynamics, which suggests it is feasible to create a generalizable controller through meta-learning. In this work, we formulate a meta reinforcement learning (meta-RL) control strategy that takes advantage of known, offline information for training, such as a model structure. The meta-RL agent is trained over a distribution of model parameters, rather than a single model, enabling the agent to automatically adapt to changes in the process dynamics while maintaining performance. A key design element is the ability to leverage model-based information offline during training, while maintaining a model-free policy structure for interacting with new environments. Our previous work has demonstrated how this approach can be applied to the industrially-relevant problem of tuning proportional-integral controllers to control first order processes. In this work, we briefly reintroduce our methodology and demonstrate how it can be extended to proportional-integral-derivative controllers and second order systems.

Almost Surely Stable Deep Dynamics

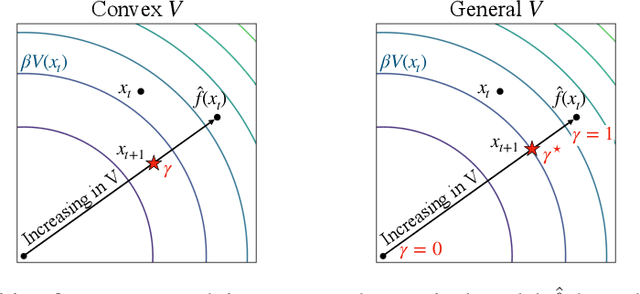
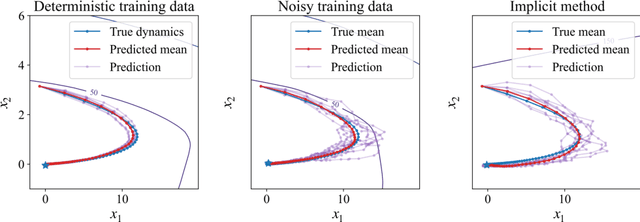
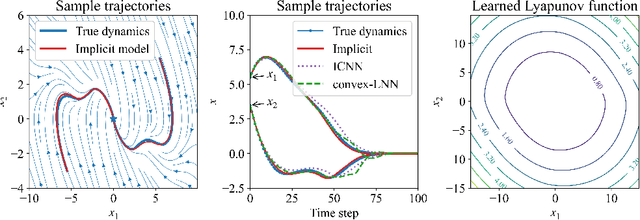
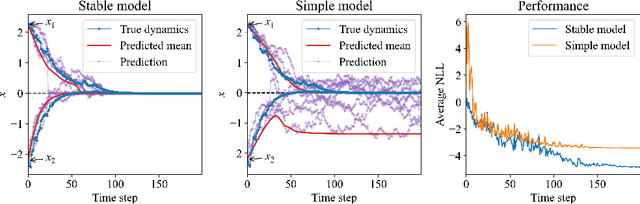
We introduce a method for learning provably stable deep neural network based dynamic models from observed data. Specifically, we consider discrete-time stochastic dynamic models, as they are of particular interest in practical applications such as estimation and control. However, these aspects exacerbate the challenge of guaranteeing stability. Our method works by embedding a Lyapunov neural network into the dynamic model, thereby inherently satisfying the stability criterion. To this end, we propose two approaches and apply them in both the deterministic and stochastic settings: one exploits convexity of the Lyapunov function, while the other enforces stability through an implicit output layer. We demonstrate the utility of each approach through numerical examples.

A Meta-Reinforcement Learning Approach to Process Control

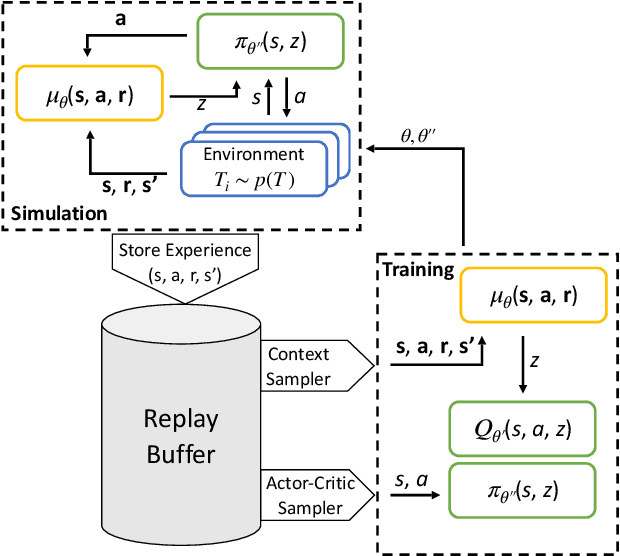
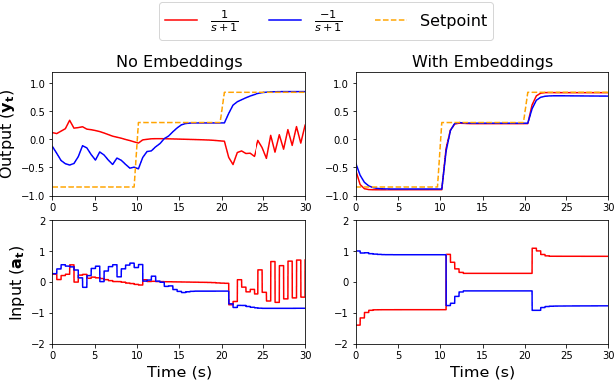
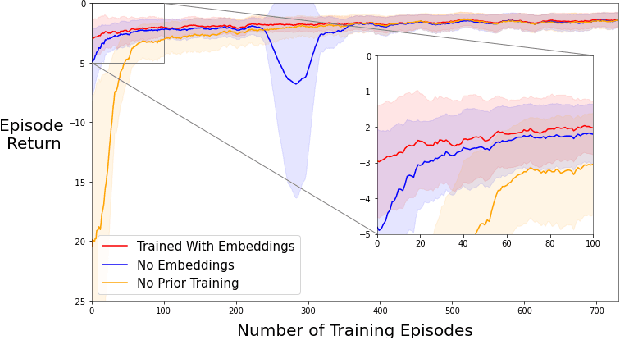
Meta-learning is a branch of machine learning which aims to quickly adapt models, such as neural networks, to perform new tasks by learning an underlying structure across related tasks. In essence, models are being trained to learn new tasks effectively rather than master a single task. Meta-learning is appealing for process control applications because the perturbations to a process required to train an AI controller can be costly and unsafe. Additionally, the dynamics and control objectives are similar across many different processes, so it is feasible to create a generalizable controller through meta-learning capable of quickly adapting to different systems. In this work, we construct a deep reinforcement learning (DRL) based controller and meta-train the controller using a latent context variable through a separate embedding neural network. We test our meta-algorithm on its ability to adapt to new process dynamics as well as different control objectives on the same process. In both cases, our meta-learning algorithm adapts very quickly to new tasks, outperforming a regular DRL controller trained from scratch. Meta-learning appears to be a promising approach for constructing more intelligent and sample-efficient controllers.