Meta Reinforcement Learning for Adaptive Control: An Offline Approach

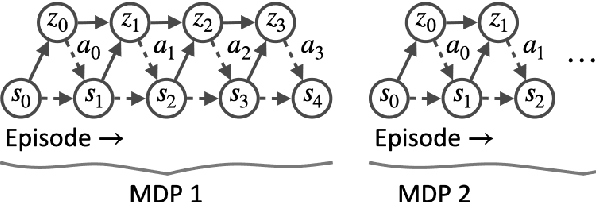
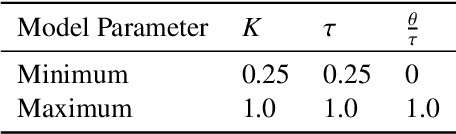
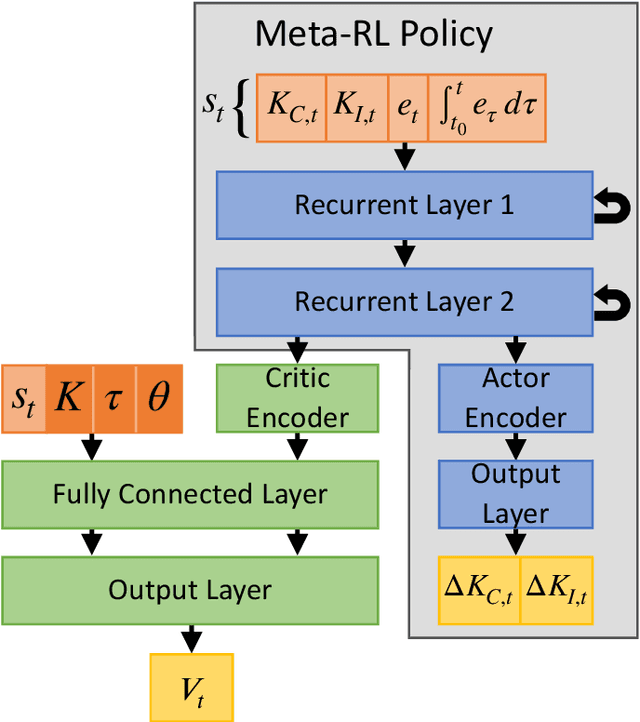
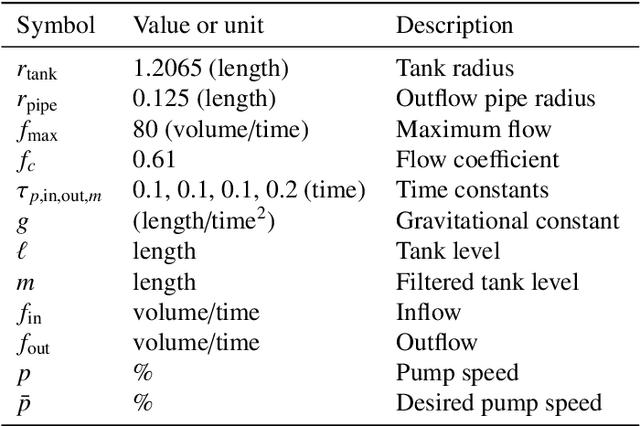
Meta-learning is a branch of machine learning which trains neural network models to synthesize a wide variety of data in order to rapidly solve new problems. In process control, many systems have similar and well-understood dynamics, which suggests it is feasible to create a generalizable controller through meta-learning. In this work, we formulate a meta reinforcement learning (meta-RL) control strategy that takes advantage of known, offline information for training, such as the system gain or time constant, yet efficiently controls novel systems in a completely model-free fashion. Our meta-RL agent has a recurrent structure that accumulates "context" for its current dynamics through a hidden state variable. This end-to-end architecture enables the agent to automatically adapt to changes in the process dynamics. Moreover, the same agent can be deployed on systems with previously unseen nonlinearities and timescales. In tests reported here, the meta-RL agent was trained entirely offline, yet produced excellent results in novel settings. A key design element is the ability to leverage model-based information offline during training, while maintaining a model-free policy structure for interacting with novel environments. To illustrate the approach, we take the actions proposed by the meta-RL agent to be changes to gains of a proportional-integral controller, resulting in a generalized, adaptive, closed-loop tuning strategy. Meta-learning is a promising approach for constructing sample-efficient intelligent controllers.

Deep Reinforcement Learning with Shallow Controllers: An Experimental Application to PID Tuning

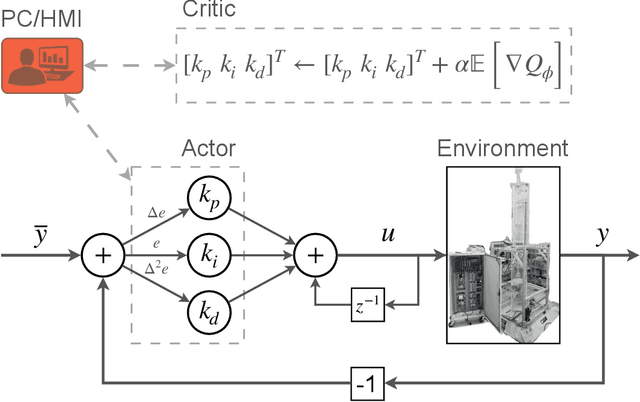
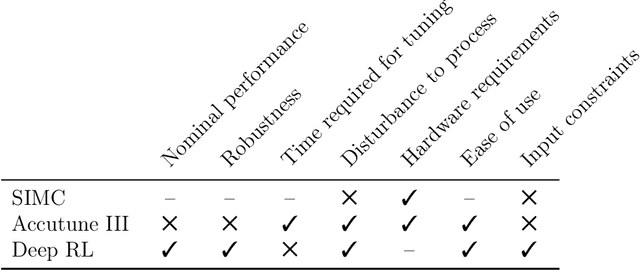
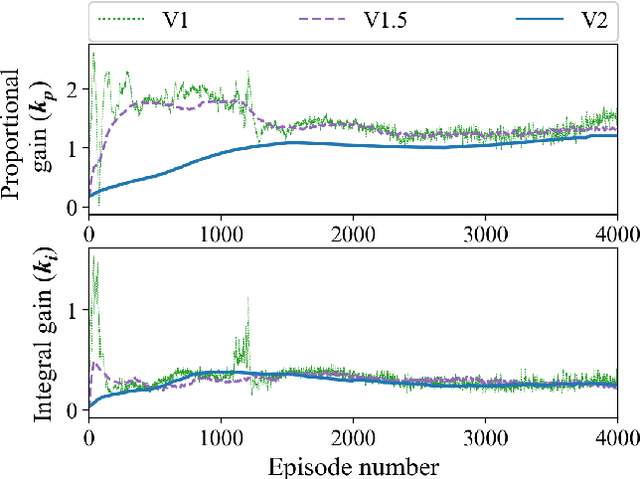
Deep reinforcement learning (RL) is an optimization-driven framework for producing control strategies for general dynamical systems without explicit reliance on process models. Good results have been reported in simulation. Here we demonstrate the challenges in implementing a state of the art deep RL algorithm on a real physical system. Aspects include the interplay between software and existing hardware; experiment design and sample efficiency; training subject to input constraints; and interpretability of the algorithm and control law. At the core of our approach is the use of a PID controller as the trainable RL policy. In addition to its simplicity, this approach has several appealing features: No additional hardware needs to be added to the control system, since a PID controller can easily be implemented through a standard programmable logic controller; the control law can easily be initialized in a "safe'' region of the parameter space; and the final product -- a well-tuned PID controller -- has a form that practitioners can reason about and deploy with confidence.

Optimal PID and Antiwindup Control Design as a Reinforcement Learning Problem

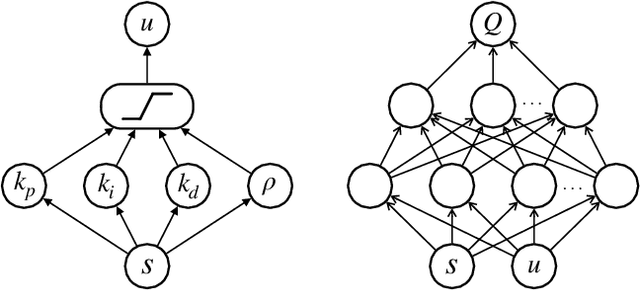
Deep reinforcement learning (DRL) has seen several successful applications to process control. Common methods rely on a deep neural network structure to model the controller or process. With increasingly complicated control structures, the closed-loop stability of such methods becomes less clear. In this work, we focus on the interpretability of DRL control methods. In particular, we view linear fixed-structure controllers as shallow neural networks embedded in the actor-critic framework. PID controllers guide our development due to their simplicity and acceptance in industrial practice. We then consider input saturation, leading to a simple nonlinear control structure. In order to effectively operate within the actuator limits we then incorporate a tuning parameter for anti-windup compensation. Finally, the simplicity of the controller allows for straightforward initialization. This makes our method inherently stabilizing, both during and after training, and amenable to known operational PID gains.

Reinforcement Learning based Design of Linear Fixed Structure Controllers

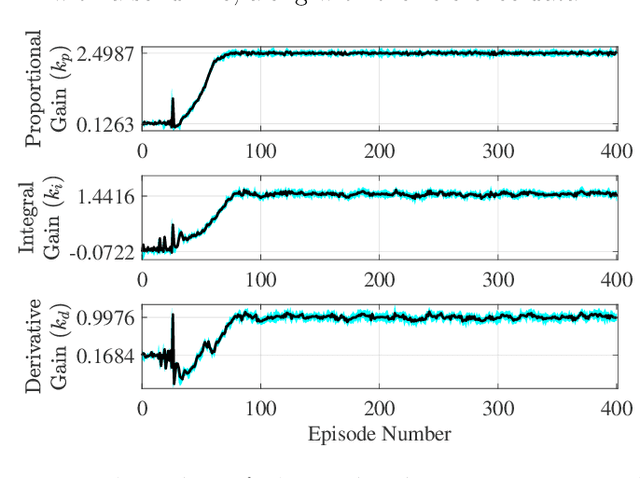
Reinforcement learning has been successfully applied to the problem of tuning PID controllers in several applications. The existing methods often utilize function approximation, such as neural networks, to update the controller parameters at each time-step of the underlying process. In this work, we present a simple finite-difference approach, based on random search, to tuning linear fixed-structure controllers. For clarity and simplicity, we focus on PID controllers. Our algorithm operates on the entire closed-loop step response of the system and iteratively improves the PID gains towards a desired closed-loop response. This allows for embedding stability requirements into the reward function without any modeling procedures.