Evaluating AI-Generated Essays with GRE Analytical Writing Assessment

The recent revolutionary advance in generative AI enables the generation of realistic and coherent texts by large language models (LLMs). Despite many existing evaluation metrics on the quality of the generated texts, there is still a lack of rigorous assessment of how well LLMs perform in complex and demanding writing assessments. This study examines essays generated by ten leading LLMs for the analytical writing assessment of the Graduate Record Exam (GRE). We assessed these essays using both human raters and the e-rater automated scoring engine as used in the GRE scoring pipeline. Notably, the top-performing Gemini and GPT-4o received an average score of 4.78 and 4.67, respectively, falling between "generally thoughtful, well-developed analysis of the issue and conveys meaning clearly" and "presents a competent analysis of the issue and conveys meaning with acceptable clarity" according to the GRE scoring guideline. We also evaluated the detection accuracy of these essays, with detectors trained on essays generated by the same and different LLMs.

The Vector Poisson Channel: On the Linearity of the Conditional Mean Estimator

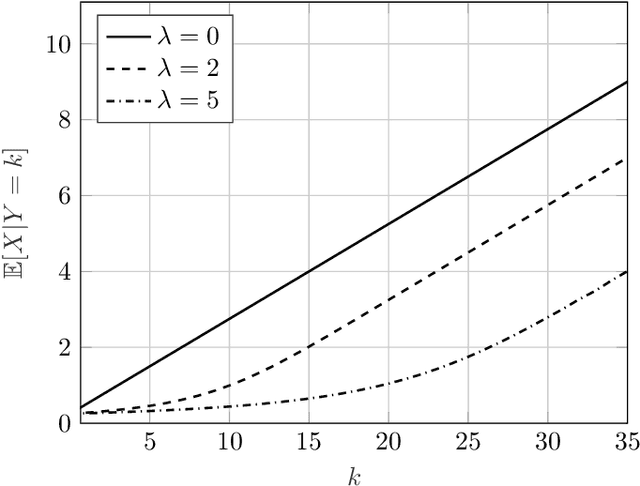
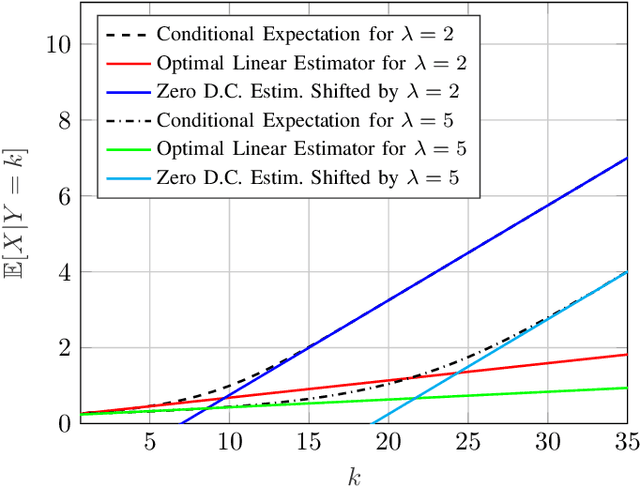
This work studies properties of the conditional mean estimator in vector Poisson noise. The main emphasis is to study conditions on prior distributions that induce linearity of the conditional mean estimator. The paper consists of two main results. The first result shows that the only distribution that induces the linearity of the conditional mean estimator is a product gamma distribution. Moreover, it is shown that the conditional mean estimator cannot be linear when the dark current parameter of the Poisson noise is non-zero. The second result produces a quantitative refinement of the first result. Specifically, it is shown that if the conditional mean estimator is close to linear in a mean squared error sense, then the prior distribution must be close to a product gamma distribution in terms of their characteristic functions. Finally, the results are compared to their Gaussian counterparts.