The Vector Poisson Channel: On the Linearity of the Conditional Mean Estimator
Paper and Code
Mar 19, 2020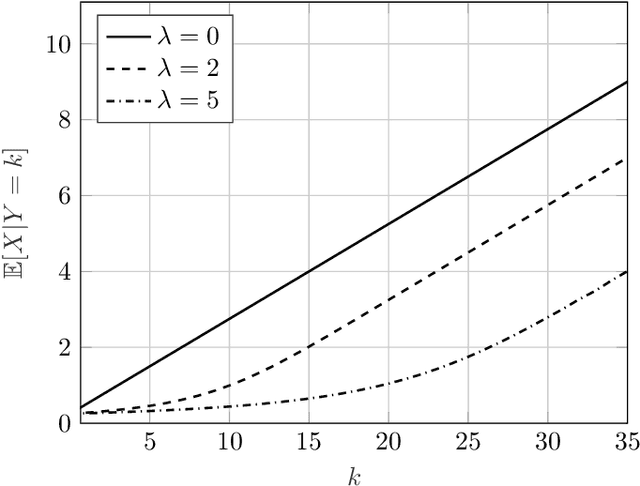
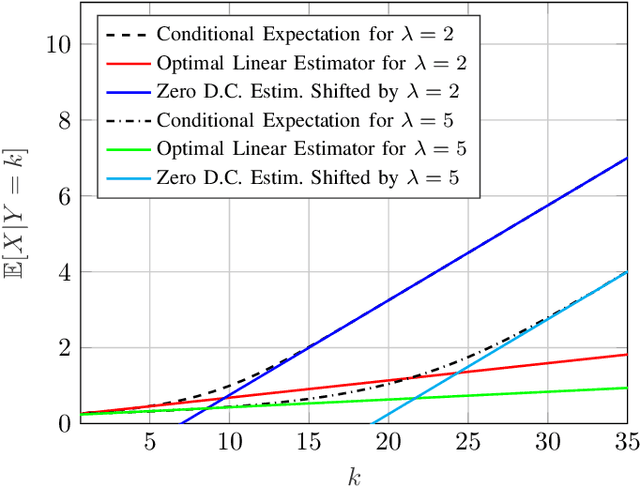
This work studies properties of the conditional mean estimator in vector Poisson noise. The main emphasis is to study conditions on prior distributions that induce linearity of the conditional mean estimator. The paper consists of two main results. The first result shows that the only distribution that induces the linearity of the conditional mean estimator is a product gamma distribution. Moreover, it is shown that the conditional mean estimator cannot be linear when the dark current parameter of the Poisson noise is non-zero. The second result produces a quantitative refinement of the first result. Specifically, it is shown that if the conditional mean estimator is close to linear in a mean squared error sense, then the prior distribution must be close to a product gamma distribution in terms of their characteristic functions. Finally, the results are compared to their Gaussian counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge