Synthetic Datasets for Machine Learning on Spatio-Temporal Graphs using PDEs

Many physical processes can be expressed through partial differential equations (PDEs). Real-world measurements of such processes are often collected at irregularly distributed points in space, which can be effectively represented as graphs; however, there are currently only a few existing datasets. Our work aims to make advancements in the field of PDE-modeling accessible to the temporal graph machine learning community, while addressing the data scarcity problem, by creating and utilizing datasets based on PDEs. In this work, we create and use synthetic datasets based on PDEs to support spatio-temporal graph modeling in machine learning for different applications. More precisely, we showcase three equations to model different types of disasters and hazards in the fields of epidemiology, atmospheric particles, and tsunami waves. Further, we show how such created datasets can be used by benchmarking several machine learning models on the epidemiological dataset. Additionally, we show how pre-training on this dataset can improve model performance on real-world epidemiological data. The presented methods enable others to create datasets and benchmarks customized to individual requirements. The source code for our methodology and the three created datasets can be found on https://github.com/github-usr-ano/Temporal_Graph_Data_PDEs.

Spatial Shortcuts in Graph Neural Controlled Differential Equations

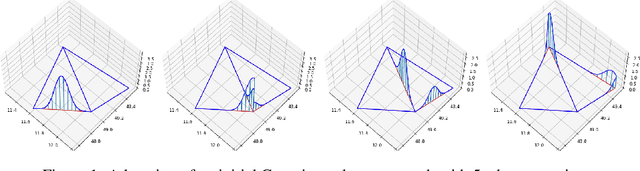
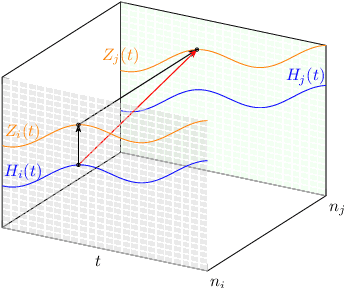
We incorporate prior graph topology information into a Neural Controlled Differential Equation (NCDE) to predict the future states of a dynamical system defined on a graph. The informed NCDE infers the future dynamics at the vertices of simulated advection data on graph edges with a known causal graph, observed only at vertices during training. We investigate different positions in the model architecture to inform the NCDE with graph information and identify an outer position between hidden state and control as theoretically and empirically favorable. Our such informed NCDE requires fewer parameters to reach a lower Mean Absolute Error (MAE) compared to previous methods that do not incorporate additional graph topology information.

Generative Fractional Diffusion Models

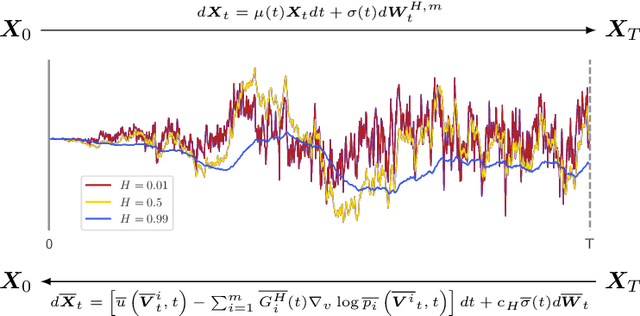
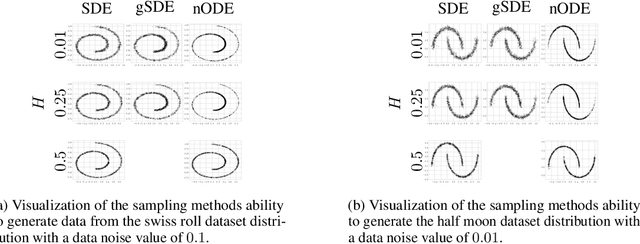
We generalize the continuous time framework for score-based generative models from an underlying Brownian motion (BM) to an approximation of fractional Brownian motion (FBM). We derive a continuous reparameterization trick and the reverse time model by representing FBM as a stochastic integral over a family of Ornstein-Uhlenbeck processes to define generative fractional diffusion models (GFDM) with driving noise converging to a non-Markovian process of infinite quadratic variation. The Hurst index $H\in(0,1)$ of FBM enables control of the roughness of the distribution transforming path. To the best of our knowledge, this is the first attempt to build a generative model upon a stochastic process with infinite quadratic variation.