Spatial Shortcuts in Graph Neural Controlled Differential Equations
Paper and Code
Oct 25, 2024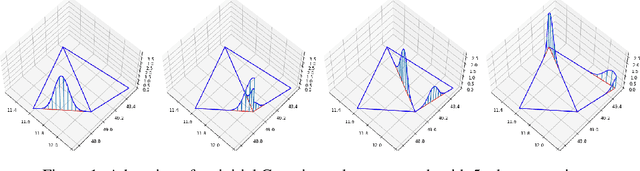

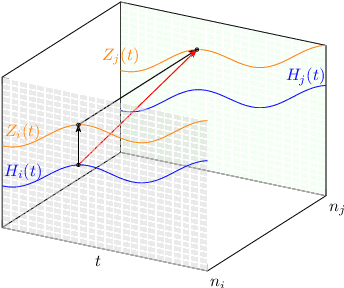

We incorporate prior graph topology information into a Neural Controlled Differential Equation (NCDE) to predict the future states of a dynamical system defined on a graph. The informed NCDE infers the future dynamics at the vertices of simulated advection data on graph edges with a known causal graph, observed only at vertices during training. We investigate different positions in the model architecture to inform the NCDE with graph information and identify an outer position between hidden state and control as theoretically and empirically favorable. Our such informed NCDE requires fewer parameters to reach a lower Mean Absolute Error (MAE) compared to previous methods that do not incorporate additional graph topology information.
* Accepted as a workshop paper at the NeurIPS 2024 workshop on
Data-driven and Differentiable Simulations, Surrogates, and Solvers (D3S3)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge