Relative Lipschitzness in Extragradient Methods and a Direct Recipe for Acceleration

We show that standard extragradient methods (i.e. mirror prox and dual extrapolation) recover optimal accelerated rates for first-order minimization of smooth convex functions. To obtain this result we provide fine-grained characterization of the convergence rates of extragradient methods for solving monotone variational inequalities in terms of a natural condition we call relative Lipschitzness. We further generalize this framework to handle local and randomized notions of relative Lipschitzness and thereby recover rates for box-constrained $\ell_\infty$ regression based on area convexity and complexity bounds achieved by accelerated (randomized) coordinate descent for smooth convex function minimization.

Sparsity, variance and curvature in multi-armed bandits

In (online) learning theory the concepts of sparsity, variance and curvature are well-understood and are routinely used to obtain refined regret and generalization bounds. In this paper we further our understanding of these concepts in the more challenging limited feedback scenario. We consider the adversarial multi-armed bandit and linear bandit settings and solve several open problems pertaining to the existence of algorithms with favorable regret bounds under the following assumptions: (i) sparsity of the individual losses, (ii) small variation of the loss sequence, and (iii) curvature of the action set. Specifically we show that (i) for $s$-sparse losses one can obtain $\tilde{O}(\sqrt{s T})$-regret (solving an open problem by Kwon and Perchet), (ii) for loss sequences with variation bounded by $Q$ one can obtain $\tilde{O}(\sqrt{Q})$-regret (solving an open problem by Kale and Hazan), and (iii) for linear bandit on an $\ell_p^n$ ball one can obtain $\tilde{O}(\sqrt{n T})$-regret for $p \in [1,2]$ and one has $\tilde{\Omega}(n \sqrt{T})$-regret for $p>2$ (solving an open problem by Bubeck, Cesa-Bianchi and Kakade). A key new insight to obtain these results is to use regularizers satisfying more refined conditions than general self-concordance

Input Sparsity Time Low-Rank Approximation via Ridge Leverage Score Sampling

We present a new algorithm for finding a near optimal low-rank approximation of a matrix $A$ in $O(nnz(A))$ time. Our method is based on a recursive sampling scheme for computing a representative subset of $A$'s columns, which is then used to find a low-rank approximation. This approach differs substantially from prior $O(nnz(A))$ time algorithms, which are all based on fast Johnson-Lindenstrauss random projections. It matches the guarantees of these methods while offering a number of advantages. Not only are sampling algorithms faster for sparse and structured data, but they can also be applied in settings where random projections cannot. For example, we give new single-pass streaming algorithms for the column subset selection and projection-cost preserving sample problems. Our method has also been used to give the fastest algorithms for provably approximating kernel matrices [MM16].

Optimal approximate matrix product in terms of stable rank

We prove, using the subspace embedding guarantee in a black box way, that one can achieve the spectral norm guarantee for approximate matrix multiplication with a dimensionality-reducing map having $m = O(\tilde{r}/\varepsilon^2)$ rows. Here $\tilde{r}$ is the maximum stable rank, i.e. squared ratio of Frobenius and operator norms, of the two matrices being multiplied. This is a quantitative improvement over previous work of [MZ11, KVZ14], and is also optimal for any oblivious dimensionality-reducing map. Furthermore, due to the black box reliance on the subspace embedding property in our proofs, our theorem can be applied to a much more general class of sketching matrices than what was known before, in addition to achieving better bounds. For example, one can apply our theorem to efficient subspace embeddings such as the Subsampled Randomized Hadamard Transform or sparse subspace embeddings, or even with subspace embedding constructions that may be developed in the future. Our main theorem, via connections with spectral error matrix multiplication shown in prior work, implies quantitative improvements for approximate least squares regression and low rank approximation. Our main result has also already been applied to improve dimensionality reduction guarantees for $k$-means clustering [CEMMP14], and implies new results for nonparametric regression [YPW15]. We also separately point out that the proof of the "BSS" deterministic row-sampling result of [BSS12] can be modified to show that for any matrices $A, B$ of stable rank at most $\tilde{r}$, one can achieve the spectral norm guarantee for approximate matrix multiplication of $A^T B$ by deterministically sampling $O(\tilde{r}/\varepsilon^2)$ rows that can be found in polynomial time. The original result of [BSS12] was for rank instead of stable rank. Our observation leads to a stronger version of a main theorem of [KMST10].

Dimensionality Reduction for k-Means Clustering and Low Rank Approximation

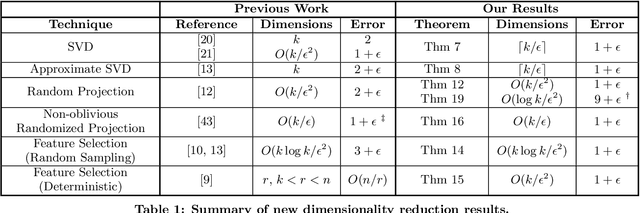
We show how to approximate a data matrix $\mathbf{A}$ with a much smaller sketch $\mathbf{\tilde A}$ that can be used to solve a general class of constrained k-rank approximation problems to within $(1+\epsilon)$ error. Importantly, this class of problems includes $k$-means clustering and unconstrained low rank approximation (i.e. principal component analysis). By reducing data points to just $O(k)$ dimensions, our methods generically accelerate any exact, approximate, or heuristic algorithm for these ubiquitous problems. For $k$-means dimensionality reduction, we provide $(1+\epsilon)$ relative error results for many common sketching techniques, including random row projection, column selection, and approximate SVD. For approximate principal component analysis, we give a simple alternative to known algorithms that has applications in the streaming setting. Additionally, we extend recent work on column-based matrix reconstruction, giving column subsets that not only `cover' a good subspace for $\bv{A}$, but can be used directly to compute this subspace. Finally, for $k$-means clustering, we show how to achieve a $(9+\epsilon)$ approximation by Johnson-Lindenstrauss projecting data points to just $O(\log k/\epsilon^2)$ dimensions. This gives the first result that leverages the specific structure of $k$-means to achieve dimension independent of input size and sublinear in $k$.

Uniform Sampling for Matrix Approximation

Random sampling has become a critical tool in solving massive matrix problems. For linear regression, a small, manageable set of data rows can be randomly selected to approximate a tall, skinny data matrix, improving processing time significantly. For theoretical performance guarantees, each row must be sampled with probability proportional to its statistical leverage score. Unfortunately, leverage scores are difficult to compute. A simple alternative is to sample rows uniformly at random. While this often works, uniform sampling will eliminate critical row information for many natural instances. We take a fresh look at uniform sampling by examining what information it does preserve. Specifically, we show that uniform sampling yields a matrix that, in some sense, well approximates a large fraction of the original. While this weak form of approximation is not enough for solving linear regression directly, it is enough to compute a better approximation. This observation leads to simple iterative row sampling algorithms for matrix approximation that run in input-sparsity time and preserve row structure and sparsity at all intermediate steps. In addition to an improved understanding of uniform sampling, our main proof introduces a structural result of independent interest: we show that every matrix can be made to have low coherence by reweighting a small subset of its rows.