Bayesian Adaptive Data Analysis Guarantees from Subgaussianity

The new field of adaptive data analysis seeks to provide algorithms and provable guarantees for models of machine learning that allow researchers to reuse their data, which normally falls outside of the usual statistical paradigm of static data analysis. In 2014, Dwork, Feldman, Hardt, Pitassi, Reingold and Roth introduced one potential model and proposed several solutions based on differential privacy. In previous work in 2016, we described a problem with this model and instead proposed a Bayesian variant, but also found that the analogous Bayesian methods cannot achieve the same statistical guarantees as in the static case. In this paper, we prove the first positive results for the Bayesian model, showing that with a Dirichlet prior, the posterior mean algorithm indeed matches the statistical guarantees of the static case. The main ingredient is a new theorem showing that the $\mathrm{Beta}(\alpha,\beta)$ distribution is subgaussian with variance proxy $O(1/(\alpha+\beta+1))$, a concentration result also of independent interest. We provide two proofs of this result: a probabilistic proof utilizing a simple condition for the raw moments of a positive random variable and a learning-theoretic proof based on considering the beta distribution as a posterior, both of which have implications to other related problems.

Challenges in Bayesian Adaptive Data Analysis

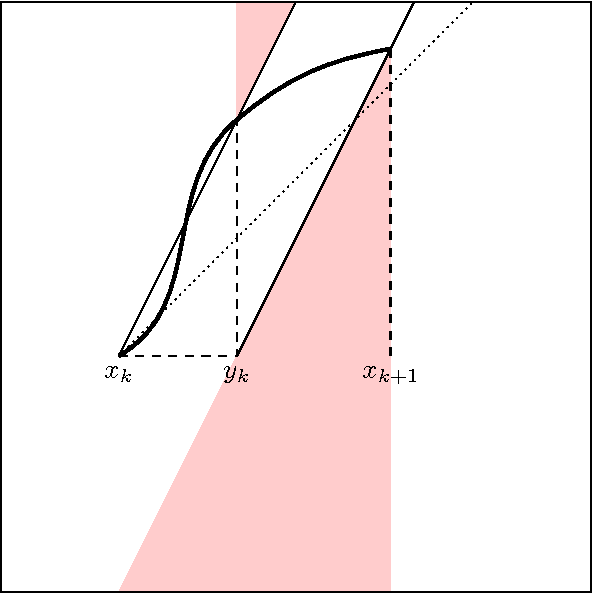
Traditional statistical analysis requires that the analysis process and data are independent. By contrast, the new field of adaptive data analysis hopes to understand and provide algorithms and accuracy guarantees for research as it is commonly performed in practice, as an iterative process of interacting repeatedly with the same data set, such as repeated tests against a holdout set. Previous work has defined a model with a rather strong lower bound on sample complexity in terms of the number of queries, $n\sim\sqrt q$, arguing that adaptive data analysis is much harder than static data analysis, where $n\sim\log q$ is possible. Instead, we argue that those strong lower bounds point to a limitation of the previous model in that it must consider wildly asymmetric scenarios which do not hold in typical applications. To better understand other difficulties of adaptivity, we propose a new Bayesian version of the problem that mandates symmetry. Since the other lower bound techniques are ruled out, we can more effectively see difficulties that might otherwise be overshadowed. As a first contribution to this model, we produce a new problem using error-correcting codes on which a large family of methods, including all previously proposed algorithms, require roughly $n\sim\sqrt[4]q$. These early results illustrate new difficulties in adaptive data analysis regarding slightly correlated queries on problems with concentrated uncertainty.

Dimensionality Reduction for k-Means Clustering and Low Rank Approximation

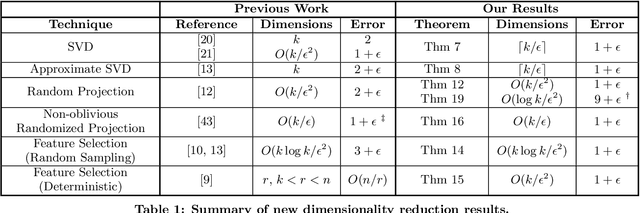
We show how to approximate a data matrix $\mathbf{A}$ with a much smaller sketch $\mathbf{\tilde A}$ that can be used to solve a general class of constrained k-rank approximation problems to within $(1+\epsilon)$ error. Importantly, this class of problems includes $k$-means clustering and unconstrained low rank approximation (i.e. principal component analysis). By reducing data points to just $O(k)$ dimensions, our methods generically accelerate any exact, approximate, or heuristic algorithm for these ubiquitous problems. For $k$-means dimensionality reduction, we provide $(1+\epsilon)$ relative error results for many common sketching techniques, including random row projection, column selection, and approximate SVD. For approximate principal component analysis, we give a simple alternative to known algorithms that has applications in the streaming setting. Additionally, we extend recent work on column-based matrix reconstruction, giving column subsets that not only `cover' a good subspace for $\bv{A}$, but can be used directly to compute this subspace. Finally, for $k$-means clustering, we show how to achieve a $(9+\epsilon)$ approximation by Johnson-Lindenstrauss projecting data points to just $O(\log k/\epsilon^2)$ dimensions. This gives the first result that leverages the specific structure of $k$-means to achieve dimension independent of input size and sublinear in $k$.