Sparse PCA from Sparse Linear Regression

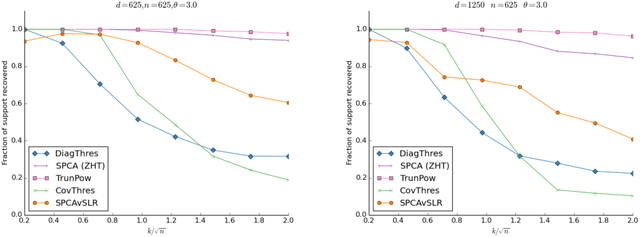
Sparse Principal Component Analysis (SPCA) and Sparse Linear Regression (SLR) have a wide range of applications and have attracted a tremendous amount of attention in the last two decades as canonical examples of statistical problems in high dimension. A variety of algorithms have been proposed for both SPCA and SLR, but an explicit connection between the two had not been made. We show how to efficiently transform a black-box solver for SLR into an algorithm for SPCA: assuming the SLR solver satisfies prediction error guarantees achieved by existing efficient algorithms such as those based on the Lasso, the SPCA algorithm derived from it achieves near state of the art guarantees for testing and for support recovery for the single spiked covariance model as obtained by the current best polynomialtime algorithms. Our reduction not only highlights the inherent similarity between the two problems, but also, from a practical standpoint, allows one to obtain a collection of algorithms for SPCA directly from known algorithms for SLR. We provide experimental results on simulated data comparing our proposed framework to other algorithms for SPCA.

Dimensionality Reduction for k-Means Clustering and Low Rank Approximation

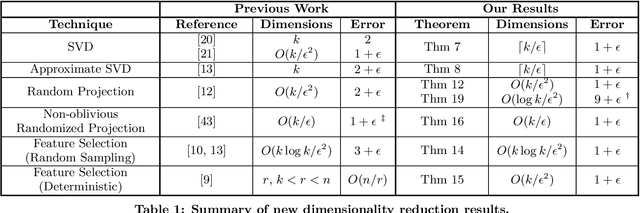
We show how to approximate a data matrix $\mathbf{A}$ with a much smaller sketch $\mathbf{\tilde A}$ that can be used to solve a general class of constrained k-rank approximation problems to within $(1+\epsilon)$ error. Importantly, this class of problems includes $k$-means clustering and unconstrained low rank approximation (i.e. principal component analysis). By reducing data points to just $O(k)$ dimensions, our methods generically accelerate any exact, approximate, or heuristic algorithm for these ubiquitous problems. For $k$-means dimensionality reduction, we provide $(1+\epsilon)$ relative error results for many common sketching techniques, including random row projection, column selection, and approximate SVD. For approximate principal component analysis, we give a simple alternative to known algorithms that has applications in the streaming setting. Additionally, we extend recent work on column-based matrix reconstruction, giving column subsets that not only `cover' a good subspace for $\bv{A}$, but can be used directly to compute this subspace. Finally, for $k$-means clustering, we show how to achieve a $(9+\epsilon)$ approximation by Johnson-Lindenstrauss projecting data points to just $O(\log k/\epsilon^2)$ dimensions. This gives the first result that leverages the specific structure of $k$-means to achieve dimension independent of input size and sublinear in $k$.