MultiNash-PF: A Particle Filtering Approach for Computing Multiple Local Generalized Nash Equilibria in Trajectory Games

Modern-world robotics involves complex environments where multiple autonomous agents must interact with each other and other humans. This necessitates advanced interactive multi-agent motion planning techniques. Generalized Nash equilibrium(GNE), a solution concept in constrained game theory, provides a mathematical model to predict the outcome of interactive motion planning, where each agent needs to account for other agents in the environment. However, in practice, multiple local GNEs may exist. Finding a single GNE itself is complex as it requires solving coupled constrained optimal control problems. Furthermore, finding all such local GNEs requires exploring the solution space of GNEs, which is a challenging task. This work proposes the MultiNash-PF framework to efficiently compute multiple local GNEs in constrained trajectory games. Potential games are a class of games for which a local GNE of a trajectory game can be found by solving a single constrained optimal control problem. We propose MultiNash-PF that integrates the potential game approach with implicit particle filtering, a sample-efficient method for non-convex trajectory optimization. We first formulate the underlying game as a constrained potential game and then utilize the implicit particle filtering to identify the coarse estimates of multiple local minimizers of the game's potential function. MultiNash-PF then refines these estimates with optimization solvers, obtaining different local GNEs. We show through numerical simulations that MultiNash-PF reduces computation time by up to 50\% compared to a baseline approach.

Understanding and Imitating Human-Robot Motion with Restricted Visual Fields

When working around humans, it is important to model their perception limitations in order to predict their behavior more accurately. In this work, we consider agents with a limited field of view, viewing range, and ability to miss objects within viewing range (e.g., transparency). By considering the observation model independently from the motion policy, we can better predict the agent's behavior by considering these limitations and approximating them. We perform a user study where human operators navigate a cluttered scene while scanning the region for obstacles with a limited field of view and range. Using imitation learning, we show that a robot can adopt a human's strategy for observing an environment with limitations on observation and navigate with minimal collision with dynamic and static obstacles. We also show that this learned model helps it successfully navigate a physical hardware vehicle in real time.

Strategic Decision-Making in Multi-Agent Domains: A Weighted Potential Dynamic Game Approach

In interactive multi-agent settings, decision-making complexity arises from agents' interconnected objectives. Dynamic game theory offers a formal framework for analyzing such intricacies. Yet, solving dynamic games and determining Nash equilibria pose computational challenges due to the need of solving coupled optimal control problems. To address this, our key idea is to leverage potential games, which are games with a potential function that allows for the computation of Nash equilibria by optimizing the potential function. We argue that dynamic potential games, can effectively facilitate interactive decision-making in many multi-agent interactions. We will identify structures in realistic multi-agent interactive scenarios that can be transformed into weighted potential dynamic games. We will show that the open-loop Nash equilibria of the resulting weighted potential dynamic game can be obtained by solving a single optimal control problem. We will demonstrate the effectiveness of the proposed method through various simulation studies, showing close proximity to feedback Nash equilibria and significant improvements in solve time compared to state-of-the-art game solvers.

Efficient Constrained Multi-Agent Interactive Planning using Constrained Dynamic Potential Games

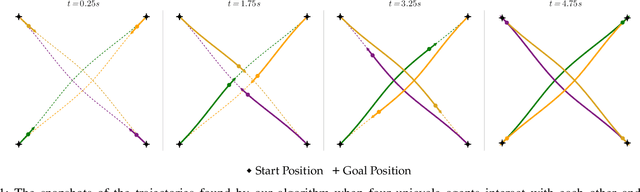
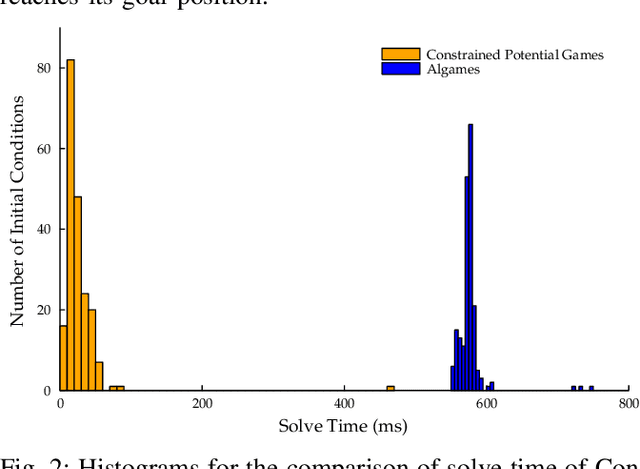
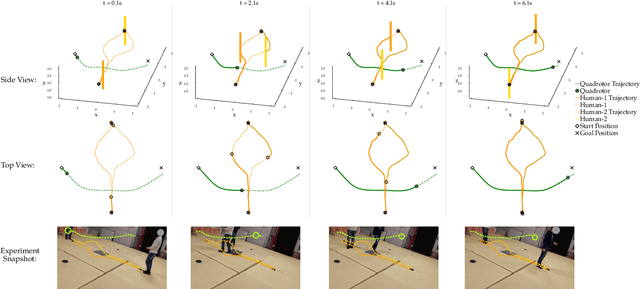
Although dynamic games provide a rich paradigm for modeling agents' interactions, solving these games for real-world applications is often challenging. Many real-wold interactive settings involve general nonlinear state and input constraints which couple agents' decisions with one another. In this work, we develop an efficient and fast planner for interactive planning in constrained setups using a constrained game-theoretical framework. Our key insight is to leverage the special structure of agents' objective and constraint functions that are common in multi-agent interactions for fast and reliable planning. More precisely, we identify the structure of agents' cost functions under which the resulting dynamic game is an instance of a constrained potential dynamic game. Constrained potential dynamic games are a class of games for which instead of solving a set of coupled constrained optimal control problems, a Nash equilibrium can be found by solving a single constrained optimal control problem. This simplifies constrained interactive trajectory planning significantly. We compare the performance of our method in a navigation setup involving four planar agents and show that our method is on average 20 times faster than the state-of-the-art. We further provide experimental validation of our proposed method in a navigation setup involving one quadrotor and two humans.