MultiNash-PF: A Particle Filtering Approach for Computing Multiple Local Generalized Nash Equilibria in Trajectory Games

Modern-world robotics involves complex environments where multiple autonomous agents must interact with each other and other humans. This necessitates advanced interactive multi-agent motion planning techniques. Generalized Nash equilibrium(GNE), a solution concept in constrained game theory, provides a mathematical model to predict the outcome of interactive motion planning, where each agent needs to account for other agents in the environment. However, in practice, multiple local GNEs may exist. Finding a single GNE itself is complex as it requires solving coupled constrained optimal control problems. Furthermore, finding all such local GNEs requires exploring the solution space of GNEs, which is a challenging task. This work proposes the MultiNash-PF framework to efficiently compute multiple local GNEs in constrained trajectory games. Potential games are a class of games for which a local GNE of a trajectory game can be found by solving a single constrained optimal control problem. We propose MultiNash-PF that integrates the potential game approach with implicit particle filtering, a sample-efficient method for non-convex trajectory optimization. We first formulate the underlying game as a constrained potential game and then utilize the implicit particle filtering to identify the coarse estimates of multiple local minimizers of the game's potential function. MultiNash-PF then refines these estimates with optimization solvers, obtaining different local GNEs. We show through numerical simulations that MultiNash-PF reduces computation time by up to 50\% compared to a baseline approach.

Model Predictive Inferential Control of Neural State-Space Models for Autonomous Vehicle Motion Planning

Model predictive control (MPC) has proven useful in enabling safe and optimal motion planning for autonomous vehicles. In this paper, we investigate how to achieve MPC-based motion planning when a neural state-space model represents the vehicle dynamics. As the neural state-space model will lead to highly complex, nonlinear and nonconvex optimization landscapes, mainstream gradient-based MPC methods will be computationally too heavy to be a viable solution. In a departure, we propose the idea of model predictive inferential control (MPIC), which seeks to infer the best control decisions from the control objectives and constraints. Following the idea, we convert the MPC problem for motion planning into a Bayesian state estimation problem. Then, we develop a new particle filtering/smoothing approach to perform the estimation. This approach is implemented as banks of unscented Kalman filters/smoothers and offers high sampling efficiency, fast computation, and estimation accuracy. We evaluate the MPIC approach through a simulation study of autonomous driving in different scenarios, along with an exhaustive comparison with gradient-based MPC. The results show that the MPIC approach has considerable computational efficiency, regardless of complex neural network architectures, and shows the capability to solve large-scale MPC problems for neural state-space models.

Model Predictive Control of Nonlinear Latent Force Models: A Scenario-Based Approach

Control of nonlinear uncertain systems is a common challenge in the robotics field. Nonlinear latent force models, which incorporate latent uncertainty characterized as Gaussian processes, carry the promise of representing such systems effectively, and we focus on the control design for them in this work. To enable the design, we adopt the state-space representation of a Gaussian process to recast the nonlinear latent force model and thus build the ability to predict the future state and uncertainty concurrently. Using this feature, a stochastic model predictive control problem is formulated. To derive a computational algorithm for the problem, we use the scenario-based approach to formulate a deterministic approximation of the stochastic optimization. We evaluate the resultant scenario-based model predictive control approach through a simulation study based on motion planning of an autonomous vehicle, which shows much effectiveness. The proposed approach can find prospective use in various other robotics applications.

Sampling-Based Nonlinear MPC of Neural Network Dynamics with Application to Autonomous Vehicle Motion Planning

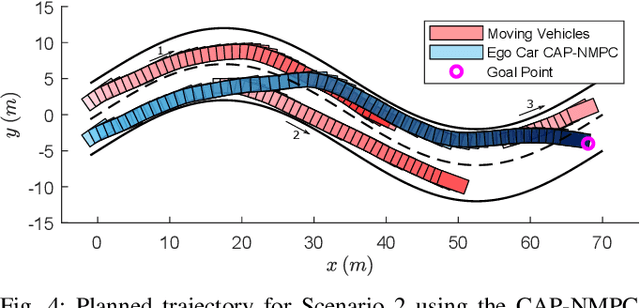
Control of machine learning models has emerged as an important paradigm for a broad range of robotics applications. In this paper, we present a sampling-based nonlinear model predictive control (NMPC) approach for control of neural network dynamics. We show its design in two parts: 1) formulating conventional optimization-based NMPC as a Bayesian state estimation problem, and 2) using particle filtering/smoothing to achieve the estimation. Through a principled sampling-based implementation, this approach can potentially make effective searches in the control action space for optimal control and also facilitate computation toward overcoming the challenges caused by neural network dynamics. We apply the proposed NMPC approach to motion planning for autonomous vehicles. The specific problem considers nonlinear unknown vehicle dynamics modeled as neural networks as well as dynamic on-road driving scenarios. The approach shows significant effectiveness in successful motion planning in case studies.