Efficient Constrained Multi-Agent Interactive Planning using Constrained Dynamic Potential Games
Paper and Code
Jun 17, 2022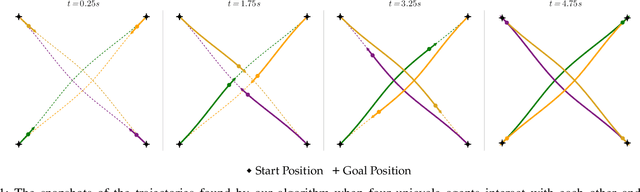
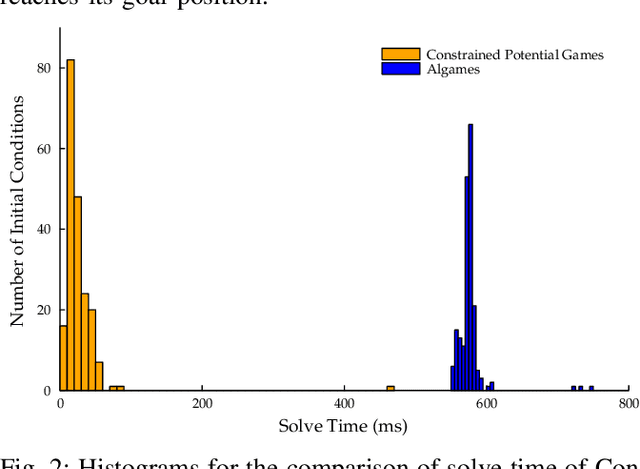
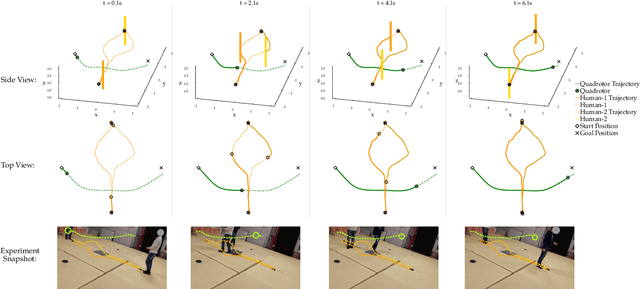
Although dynamic games provide a rich paradigm for modeling agents' interactions, solving these games for real-world applications is often challenging. Many real-wold interactive settings involve general nonlinear state and input constraints which couple agents' decisions with one another. In this work, we develop an efficient and fast planner for interactive planning in constrained setups using a constrained game-theoretical framework. Our key insight is to leverage the special structure of agents' objective and constraint functions that are common in multi-agent interactions for fast and reliable planning. More precisely, we identify the structure of agents' cost functions under which the resulting dynamic game is an instance of a constrained potential dynamic game. Constrained potential dynamic games are a class of games for which instead of solving a set of coupled constrained optimal control problems, a Nash equilibrium can be found by solving a single constrained optimal control problem. This simplifies constrained interactive trajectory planning significantly. We compare the performance of our method in a navigation setup involving four planar agents and show that our method is on average 20 times faster than the state-of-the-art. We further provide experimental validation of our proposed method in a navigation setup involving one quadrotor and two humans.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge