The Dynamic-Probabilistic Consistency Gap in Chaotic Surrogate Modeling

Dynamical systems reconstruction (DSR) aims to learn surrogate models that capture the dynamics underlying time-series data. Reliably deploying these surrogates requires uncertainty estimates consistent with the learned dynamics. We expose a dynamic-probabilistic consistency (DPC) gap: the pursuit of finite-horizon probabilistic objectives can degrade dynamics or decouple predictive uncertainty from the local tangent dynamics it ought to reflect. We isolate three mechanisms behind this gap: core collapse, noise masking, and blind uncertainty. Specifically, we show that open-loop Gaussian rollout objectives can penalize Jacobian-generated covariance growth in chaotic systems, encouraging optimization shortcuts that weaken physical expansion or decouple uncertainty from it. To mitigate this gap, we propose KAFFEE (Kalman-Aware Framework For Ergodic Emulation), a differentiable extended Kalman filter-based training framework that evaluates likelihood on local predictive residuals (innovations) while transporting covariance through learned local Jacobians. On stochastic hyperchaotic Lorenz-96, KAFFEE reduces the identified failure modes, improves reconstruction of dynamical invariants relative to open-loop objectives, and maintains competitive predictive scores. We further show that the DPC gap appears when probabilistically adapting a DSR foundation model across 13 chaotic systems, where KAFFEE enables in-context Bayesian filtering while largely preserving zero-shot dynamics.

sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

Inferring stochastic low-rank recurrent neural networks from neural data

A central aim in computational neuroscience is to relate the activity of large populations of neurons to an underlying dynamical system. Models of these neural dynamics should ideally be both interpretable and fit the observed data well. Low-rank recurrent neural networks (RNNs) exhibit such interpretability by having tractable dynamics. However, it is unclear how to best fit low-rank RNNs to data consisting of noisy observations of an underlying stochastic system. Here, we propose to fit stochastic low-rank RNNs with variational sequential Monte Carlo methods. We validate our method on several datasets consisting of both continuous and spiking neural data, where we obtain lower dimensional latent dynamics than current state of the art methods. Additionally, for low-rank models with piecewise linear nonlinearities, we show how to efficiently identify all fixed points in polynomial rather than exponential cost in the number of units, making analysis of the inferred dynamics tractable for large RNNs. Our method both elucidates the dynamical systems underlying experimental recordings and provides a generative model whose trajectories match observed trial-to-trial variability.

A Practical Guide to Statistical Distances for Evaluating Generative Models in Science

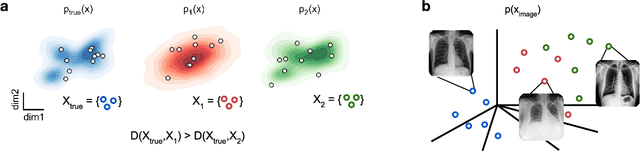
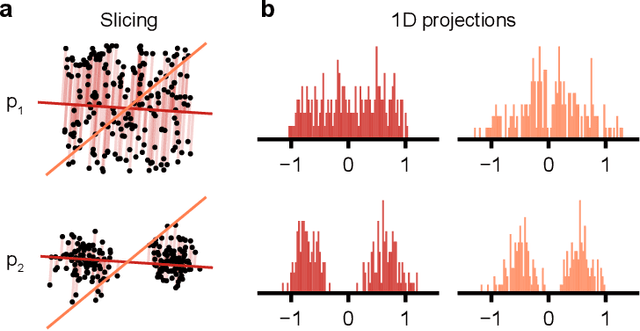
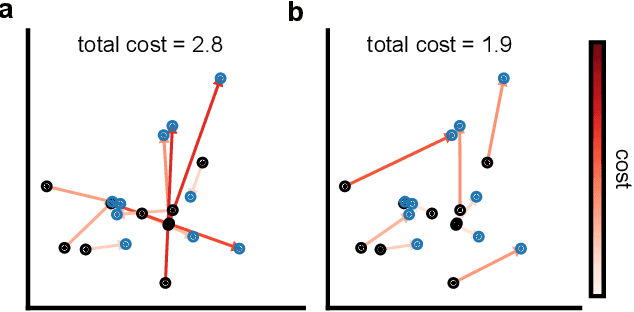
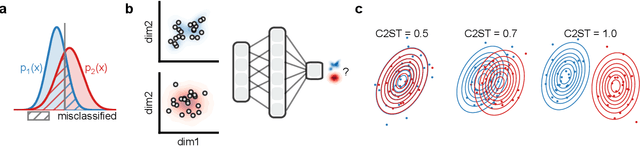
Generative models are invaluable in many fields of science because of their ability to capture high-dimensional and complicated distributions, such as photo-realistic images, protein structures, and connectomes. How do we evaluate the samples these models generate? This work aims to provide an accessible entry point to understanding popular notions of statistical distances, requiring only foundational knowledge in mathematics and statistics. We focus on four commonly used notions of statistical distances representing different methodologies: Using low-dimensional projections (Sliced-Wasserstein; SW), obtaining a distance using classifiers (Classifier Two-Sample Tests; C2ST), using embeddings through kernels (Maximum Mean Discrepancy; MMD), or neural networks (Fr\'echet Inception Distance; FID). We highlight the intuition behind each distance and explain their merits, scalability, complexity, and pitfalls. To demonstrate how these distances are used in practice, we evaluate generative models from different scientific domains, namely a model of decision making and a model generating medical images. We showcase that distinct distances can give different results on similar data. Through this guide, we aim to help researchers to use, interpret, and evaluate statistical distances for generative models in science.