Optimal Classification-based Anomaly Detection with Neural Networks: Theory and Practice

Anomaly detection is an important problem in many application areas, such as network security. Many deep learning methods for unsupervised anomaly detection produce good empirical performance but lack theoretical guarantees. By casting anomaly detection into a binary classification problem, we establish non-asymptotic upper bounds and a convergence rate on the excess risk on rectified linear unit (ReLU) neural networks trained on synthetic anomalies. Our convergence rate on the excess risk matches the minimax optimal rate in the literature. Furthermore, we provide lower and upper bounds on the number of synthetic anomalies that can attain this optimality. For practical implementation, we relax some conditions to improve the search for the empirical risk minimizer, which leads to competitive performance to other classification-based methods for anomaly detection. Overall, our work provides the first theoretical guarantees of unsupervised neural network-based anomaly detectors and empirical insights on how to design them well.

Non-Robust Features are Not Always Useful in One-Class Classification

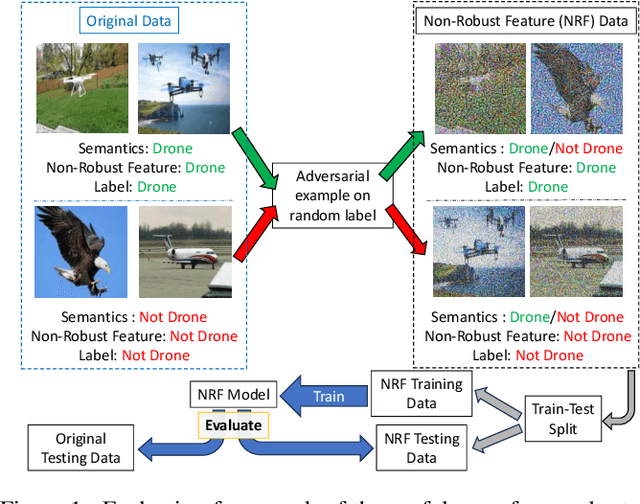
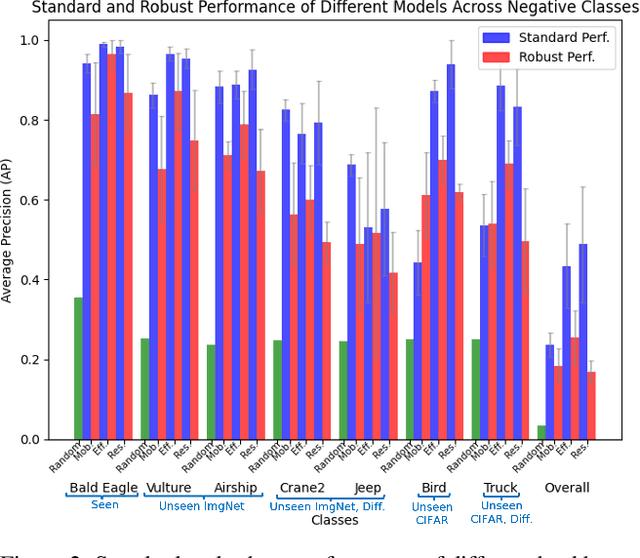
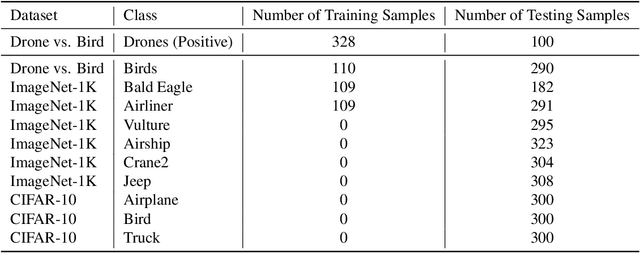
The robustness of machine learning models has been questioned by the existence of adversarial examples. We examine the threat of adversarial examples in practical applications that require lightweight models for one-class classification. Building on Ilyas et al. (2019), we investigate the vulnerability of lightweight one-class classifiers to adversarial attacks and possible reasons for it. Our results show that lightweight one-class classifiers learn features that are not robust (e.g. texture) under stronger attacks. However, unlike in multi-class classification (Ilyas et al., 2019), these non-robust features are not always useful for the one-class task, suggesting that learning these unpredictive and non-robust features is an unwanted consequence of training.

Revisiting Non-separable Binary Classification and its Applications in Anomaly Detection

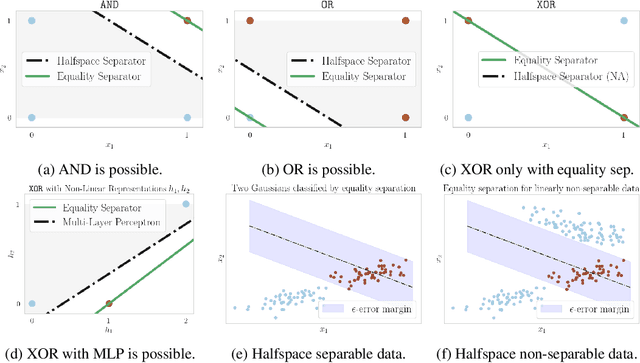
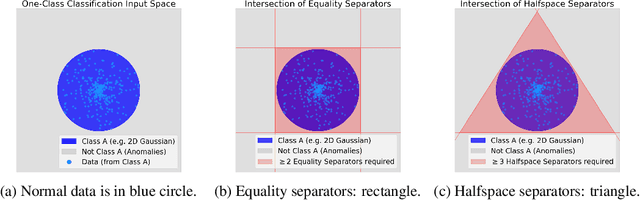
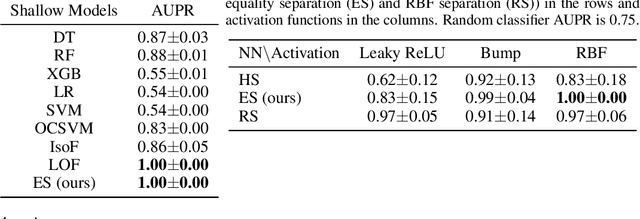
The inability to linearly classify XOR has motivated much of deep learning. We revisit this age-old problem and show that linear classification of XOR is indeed possible. Instead of separating data between halfspaces, we propose a slightly different paradigm, equality separation, that adapts the SVM objective to distinguish data within or outside the margin. Our classifier can then be integrated into neural network pipelines with a smooth approximation. From its properties, we intuit that equality separation is suitable for anomaly detection. To formalize this notion, we introduce closing numbers, a quantitative measure on the capacity for classifiers to form closed decision regions for anomaly detection. Springboarding from this theoretical connection between binary classification and anomaly detection, we test our hypothesis on supervised anomaly detection experiments, showing that equality separation can detect both seen and unseen anomalies.