Optimal Classification-based Anomaly Detection with Neural Networks: Theory and Practice

Anomaly detection is an important problem in many application areas, such as network security. Many deep learning methods for unsupervised anomaly detection produce good empirical performance but lack theoretical guarantees. By casting anomaly detection into a binary classification problem, we establish non-asymptotic upper bounds and a convergence rate on the excess risk on rectified linear unit (ReLU) neural networks trained on synthetic anomalies. Our convergence rate on the excess risk matches the minimax optimal rate in the literature. Furthermore, we provide lower and upper bounds on the number of synthetic anomalies that can attain this optimality. For practical implementation, we relax some conditions to improve the search for the empirical risk minimizer, which leads to competitive performance to other classification-based methods for anomaly detection. Overall, our work provides the first theoretical guarantees of unsupervised neural network-based anomaly detectors and empirical insights on how to design them well.

Approximation of RKHS Functionals by Neural Networks

Motivated by the abundance of functional data such as time series and images, there has been a growing interest in integrating such data into neural networks and learning maps from function spaces to R (i.e., functionals). In this paper, we study the approximation of functionals on reproducing kernel Hilbert spaces (RKHS's) using neural networks. We establish the universality of the approximation of functionals on the RKHS's. Specifically, we derive explicit error bounds for those induced by inverse multiquadric, Gaussian, and Sobolev kernels. Moreover, we apply our findings to functional regression, proving that neural networks can accurately approximate the regression maps in generalized functional linear models. Existing works on functional learning require integration-type basis function expansions with a set of pre-specified basis functions. By leveraging the interpolating orthogonal projections in RKHS's, our proposed network is much simpler in that we use point evaluations to replace basis function expansions.

Classification of Data Generated by Gaussian Mixture Models Using Deep ReLU Networks

This paper studies the binary classification of unbounded data from ${\mathbb R}^d$ generated under Gaussian Mixture Models (GMMs) using deep ReLU neural networks. We obtain $\unicode{x2013}$ for the first time $\unicode{x2013}$ non-asymptotic upper bounds and convergence rates of the excess risk (excess misclassification error) for the classification without restrictions on model parameters. The convergence rates we derive do not depend on dimension $d$, demonstrating that deep ReLU networks can overcome the curse of dimensionality in classification. While the majority of existing generalization analysis of classification algorithms relies on a bounded domain, we consider an unbounded domain by leveraging the analyticity and fast decay of Gaussian distributions. To facilitate our analysis, we give a novel approximation error bound for general analytic functions using ReLU networks, which may be of independent interest. Gaussian distributions can be adopted nicely to model data arising in applications, e.g., speeches, images, and texts; our results provide a theoretical verification of the observed efficiency of deep neural networks in practical classification problems.

Learning Ability of Interpolating Convolutional Neural Networks

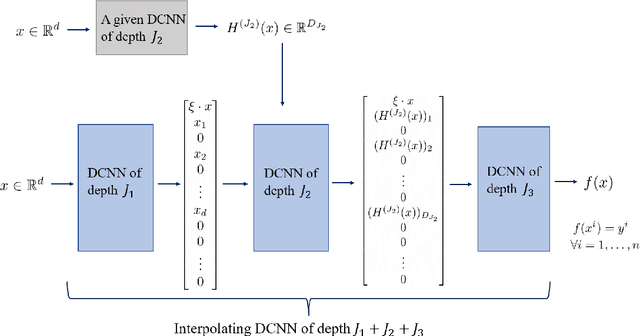
It is frequently observed that overparameterized neural networks generalize well. Regarding such phenomena, existing theoretical work mainly devotes to linear settings or fully connected neural networks. This paper studies learning ability of an important family of deep neural networks, deep convolutional neural networks (DCNNs), under underparameterized and overparameterized settings. We establish the best learning rates of underparameterized DCNNs without parameter restrictions presented in the literature. We also show that, by adding well defined layers to an underparameterized DCNN, we can obtain some interpolating DCNNs that maintain the good learning rates of the underparameterized DCNN. This result is achieved by a novel network deepening scheme designed for DCNNs. Our work provides theoretical verification on how overfitted DCNNs generalize well.