Inherent Weight Normalization in Stochastic Neural Networks

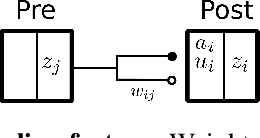
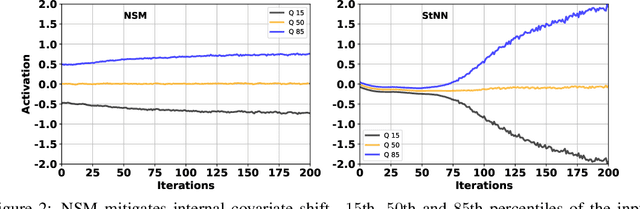
Multiplicative stochasticity such as Dropout improves the robustness and generalizability of deep neural networks. Here, we further demonstrate that always-on multiplicative stochasticity combined with simple threshold neurons are sufficient operations for deep neural networks. We call such models Neural Sampling Machines (NSM). We find that the probability of activation of the NSM exhibits a self-normalizing property that mirrors Weight Normalization, a previously studied mechanism that fulfills many of the features of Batch Normalization in an online fashion. The normalization of activities during training speeds up convergence by preventing internal covariate shift caused by changes in the input distribution. The always-on stochasticity of the NSM confers the following advantages: the network is identical in the inference and learning phases, making the NSM suitable for online learning, it can exploit stochasticity inherent to a physical substrate such as analog non-volatile memories for in-memory computing, and it is suitable for Monte Carlo sampling, while requiring almost exclusively addition and comparison operations. We demonstrate NSMs on standard classification benchmarks (MNIST and CIFAR) and event-based classification benchmarks (N-MNIST and DVS Gestures). Our results show that NSMs perform comparably or better than conventional artificial neural networks with the same architecture.

Design space exploration of Ferroelectric FET based Processing-in-Memory DNN Accelerator

In this letter, we quantify the impact of device limitations on the classification accuracy of an artificial neural network, where the synaptic weights are implemented in a Ferroelectric FET (FeFET) based in-memory processing architecture. We explore a design-space consisting of the resolution of the analog-to-digital converter, number of bits per FeFET cell, and the neural network depth. We show how the system architecture, training models and overparametrization can address some of the device limitations.

Stochastic IMT (insulator-metal-transition) neurons: An interplay of thermal and threshold noise at bifurcation

Artificial neural networks can harness stochasticity in multiple ways to enable a vast class of computationally powerful models. Electronic implementation of such stochastic networks is currently limited to addition of algorithmic noise to digital machines which is inherently inefficient; albeit recent efforts to harness physical noise in devices for stochasticity have shown promise. To succeed in fabricating electronic neuromorphic networks we need experimental evidence of devices with measurable and controllable stochasticity which is complemented with the development of reliable statistical models of such observed stochasticity. Current research literature has sparse evidence of the former and a complete lack of the latter. This motivates the current article where we demonstrate a stochastic neuron using an insulator-metal-transition (IMT) device, based on electrically induced phase-transition, in series with a tunable resistance. We show that an IMT neuron has dynamics similar to a piecewise linear FitzHugh-Nagumo (FHN) neuron and incorporates all characteristics of a spiking neuron in the device phenomena. We experimentally demonstrate spontaneous stochastic spiking along with electrically controllable firing probabilities using Vanadium Dioxide (VO$_2$) based IMT neurons which show a sigmoid-like transfer function. The stochastic spiking is explained by two noise sources - thermal noise and threshold fluctuations, which act as precursors of bifurcation. As such, the IMT neuron is modeled as an Ornstein-Uhlenbeck (OU) process with a fluctuating boundary resulting in transfer curves that closely match experiments. As one of the first comprehensive studies of a stochastic neuron hardware and its statistical properties, this article would enable efficient implementation of a large class of neuro-mimetic networks and algorithms.