Neural Sampling Machine with Stochastic Synapse allows Brain-like Learning and Inference

Many real-world mission-critical applications require continual online learning from noisy data and real-time decision making with a defined confidence level. Probabilistic models and stochastic neural networks can explicitly handle uncertainty in data and allow adaptive learning-on-the-fly, but their implementation in a low-power substrate remains a challenge. Here, we introduce a novel hardware fabric that implements a new class of stochastic NN called Neural-Sampling-Machine that exploits stochasticity in synaptic connections for approximate Bayesian inference. Harnessing the inherent non-linearities and stochasticity occurring at the atomic level in emerging materials and devices allows us to capture the synaptic stochasticity occurring at the molecular level in biological synapses. We experimentally demonstrate in-silico hybrid stochastic synapse by pairing a ferroelectric field-effect transistor -based analog weight cell with a two-terminal stochastic selector element. Such a stochastic synapse can be integrated within the well-established crossbar array architecture for compute-in-memory. We experimentally show that the inherent stochastic switching of the selector element between the insulator and metallic state introduces a multiplicative stochastic noise within the synapses of NSM that samples the conductance states of the FeFET, both during learning and inference. We perform network-level simulations to highlight the salient automatic weight normalization feature introduced by the stochastic synapses of the NSM that paves the way for continual online learning without any offline Batch Normalization. We also showcase the Bayesian inferencing capability introduced by the stochastic synapse during inference mode, thus accounting for uncertainty in data. We report 98.25%accuracy on standard image classification task as well as estimation of data uncertainty in rotated samples.

Inherent Weight Normalization in Stochastic Neural Networks

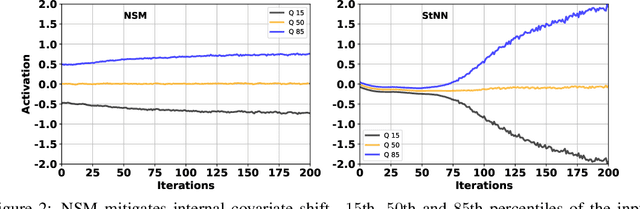
Multiplicative stochasticity such as Dropout improves the robustness and generalizability of deep neural networks. Here, we further demonstrate that always-on multiplicative stochasticity combined with simple threshold neurons are sufficient operations for deep neural networks. We call such models Neural Sampling Machines (NSM). We find that the probability of activation of the NSM exhibits a self-normalizing property that mirrors Weight Normalization, a previously studied mechanism that fulfills many of the features of Batch Normalization in an online fashion. The normalization of activities during training speeds up convergence by preventing internal covariate shift caused by changes in the input distribution. The always-on stochasticity of the NSM confers the following advantages: the network is identical in the inference and learning phases, making the NSM suitable for online learning, it can exploit stochasticity inherent to a physical substrate such as analog non-volatile memories for in-memory computing, and it is suitable for Monte Carlo sampling, while requiring almost exclusively addition and comparison operations. We demonstrate NSMs on standard classification benchmarks (MNIST and CIFAR) and event-based classification benchmarks (N-MNIST and DVS Gestures). Our results show that NSMs perform comparably or better than conventional artificial neural networks with the same architecture.