Direct Feedback Alignment with Sparse Connections for Local Learning

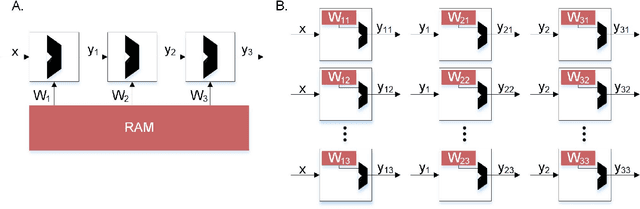
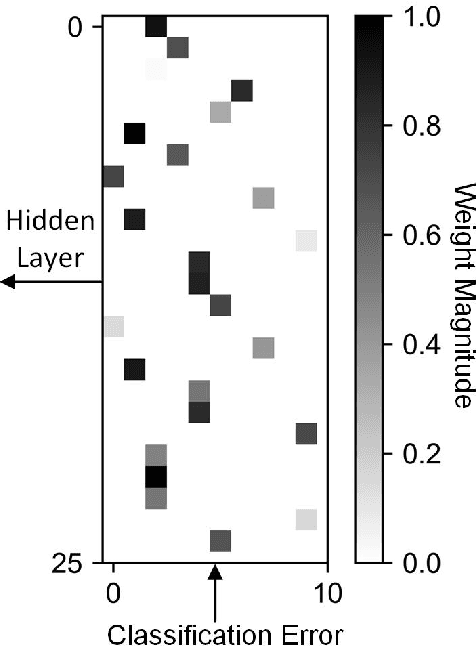
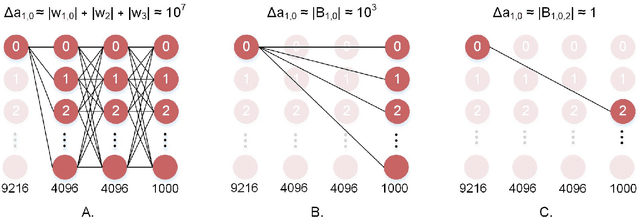
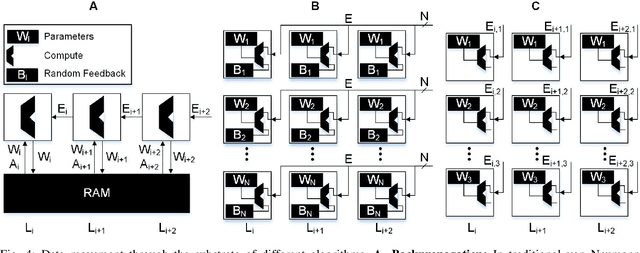
Recent advances in deep neural networks (DNNs) owe their success to training algorithms that use backpropagation and gradient-descent. Backpropagation, while highly effective on von Neumann architectures, becomes inefficient when scaling to large networks. Commonly referred to as the weight transport problem, each neuron's dependence on the weights and errors located deeper in the network require exhaustive data movement which presents a key problem in enhancing the performance and energy-efficiency of machine-learning hardware. In this work, we propose a bio-plausible alternative to backpropagation drawing from advances in feedback alignment algorithms in which the error computation at a single synapse reduces to the product of three scalar values, satisfying the three factor rule. Using a sparse feedback matrix, we show that a neuron needs only a fraction of the information previously used by the feedback alignment algorithms to yield results which are competitive with backpropagation. Consequently, memory and compute can be partitioned and distributed whichever way produces the most efficient forward pass so long as a single error can be delivered to each neuron. We evaluate our algorithm using standard data sets, including ImageNet, to address the concern of scaling to challenging problems. Our results show orders of magnitude improvement in data movement and 2x improvement in multiply-and-accumulate operations over backpropagation. All the code and results are available under https://github.com/bcrafton/ssdfa.

Stochastic IMT (insulator-metal-transition) neurons: An interplay of thermal and threshold noise at bifurcation

Artificial neural networks can harness stochasticity in multiple ways to enable a vast class of computationally powerful models. Electronic implementation of such stochastic networks is currently limited to addition of algorithmic noise to digital machines which is inherently inefficient; albeit recent efforts to harness physical noise in devices for stochasticity have shown promise. To succeed in fabricating electronic neuromorphic networks we need experimental evidence of devices with measurable and controllable stochasticity which is complemented with the development of reliable statistical models of such observed stochasticity. Current research literature has sparse evidence of the former and a complete lack of the latter. This motivates the current article where we demonstrate a stochastic neuron using an insulator-metal-transition (IMT) device, based on electrically induced phase-transition, in series with a tunable resistance. We show that an IMT neuron has dynamics similar to a piecewise linear FitzHugh-Nagumo (FHN) neuron and incorporates all characteristics of a spiking neuron in the device phenomena. We experimentally demonstrate spontaneous stochastic spiking along with electrically controllable firing probabilities using Vanadium Dioxide (VO$_2$) based IMT neurons which show a sigmoid-like transfer function. The stochastic spiking is explained by two noise sources - thermal noise and threshold fluctuations, which act as precursors of bifurcation. As such, the IMT neuron is modeled as an Ornstein-Uhlenbeck (OU) process with a fluctuating boundary resulting in transfer curves that closely match experiments. As one of the first comprehensive studies of a stochastic neuron hardware and its statistical properties, this article would enable efficient implementation of a large class of neuro-mimetic networks and algorithms.