Research Note on Uncertain Probabilities and Abstract Argumentation

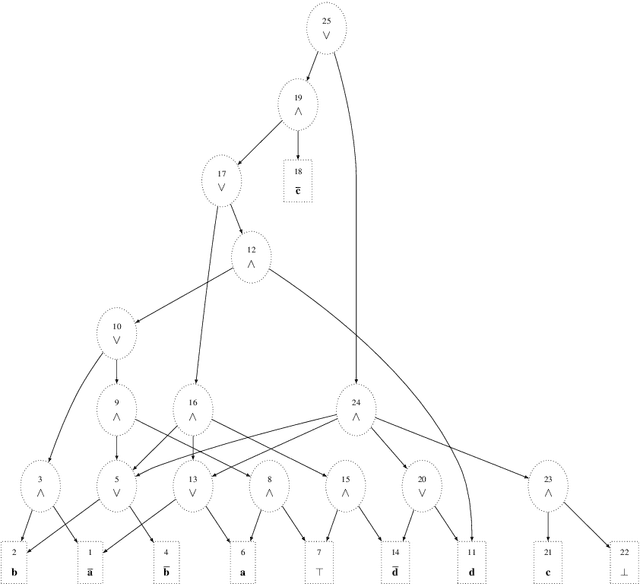
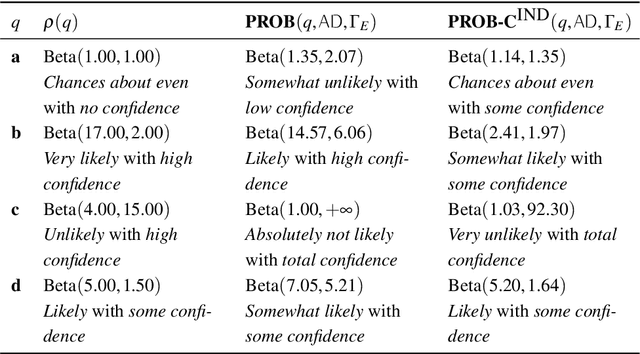
The sixth assessment of the international panel on climate change (IPCC) states that "cumulative net CO2 emissions over the last decade (2010-2019) are about the same size as the 11 remaining carbon budget likely to limit warming to 1.5C (medium confidence)." Such reports directly feed the public discourse, but nuances such as the degree of belief and of confidence are often lost. In this paper, we propose a formal account for allowing such degrees of belief and the associated confidence to be used to label arguments in abstract argumentation settings. Differently from other proposals in probabilistic argumentation, we focus on the task of probabilistic inference over a chosen query building upon Sato's distribution semantics which has been already shown to encompass a variety of cases including the semantics of Bayesian networks. Borrowing from the vast literature on such semantics, we examine how such tasks can be dealt with in practice when considering uncertain probabilities, and discuss the connections with existing proposals for probabilistic argumentation.

Automata for Infinite Argumentation Structures

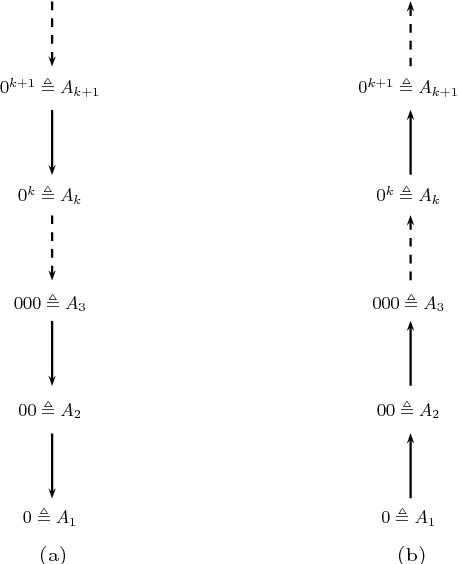
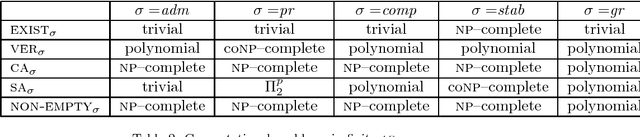
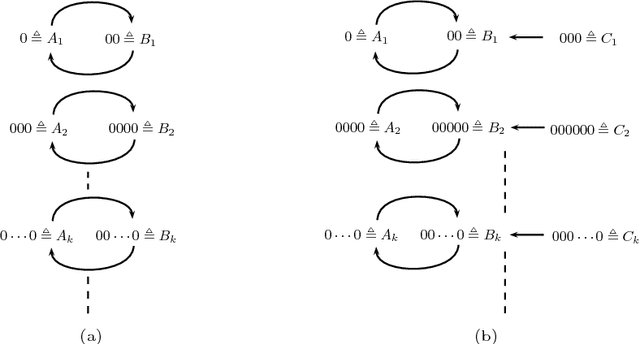
The theory of abstract argumentation frameworks (afs) has, in the main, focused on finite structures, though there are many significant contexts where argumentation can be regarded as a process involving infinite objects. To address this limitation, in this paper we propose a novel approach for describing infinite afs using tools from formal language theory. In particular, the possibly infinite set of arguments is specified through the language recognized by a deterministic finite automaton while a suitable formalism, called attack expression, is introduced to describe the relation of attack between arguments. The proposed approach is shown to satisfy some desirable properties which can not be achieved through other "naive" uses of formal languages. In particular, the approach is shown to be expressive enough to capture (besides any arbitrary finite structure) a large variety of infinite afs including two major examples from previous literature and two sample cases from the domains of multi-agent negotiation and ambient intelligence. On the computational side, we show that several decision and construction problems which are known to be polynomial time solvable in finite afs are decidable in the context of the proposed formalism and we provide the relevant algorithms. Moreover we obtain additional results concerning the case of finitary afs.

AFRA: Argumentation framework with recursive attacks

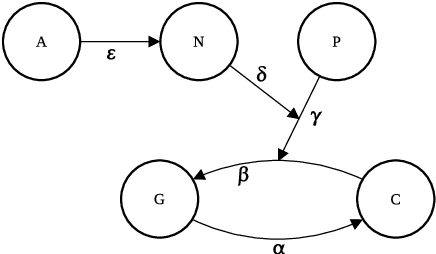
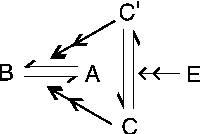
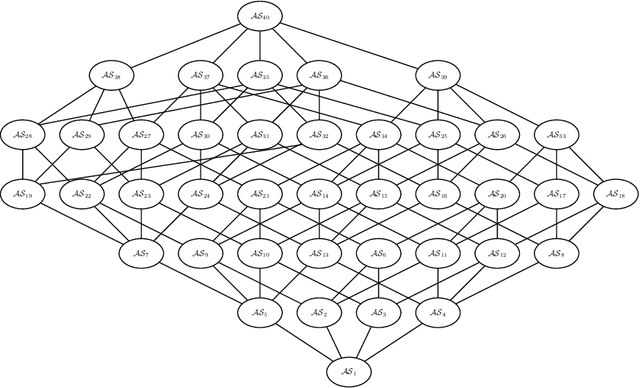
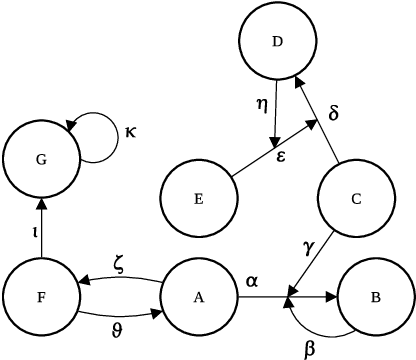
The issue of representing attacks to attacks in argumentation is receiving an increasing attention as a useful conceptual modelling tool in several contexts. In this paper we present AFRA, a formalism encompassing unlimited recursive attacks within argumentation frameworks. AFRA satisfies the basic requirements of definition simplicity and rigorous compatibility with Dung's theory of argumentation. This paper provides a complete development of the AFRA formalism complemented by illustrative examples and a detailed comparison with other recursive attack formalizations.

Solving Set Optimization Problems by Cardinality Optimization via Weak Constraints with an Application to Argumentation

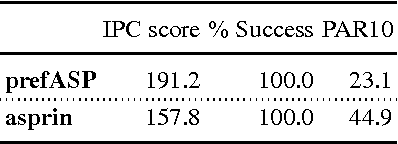
Optimization - minimization or maximization - in the lattice of subsets is a frequent operation in Artificial Intelligence tasks. Examples are subset-minimal model-based diagnosis, nonmonotonic reasoning by means of circumscription, or preferred extensions in abstract argumentation. Finding the optimum among many admissible solutions is often harder than finding admissible solutions with respect to both computational complexity and methodology. This paper addresses the former issue by means of an effective method for finding subset-optimal solutions. It is based on the relationship between cardinality-optimal and subset-optimal solutions, and the fact that many logic-based declarative programming systems provide constructs for finding cardinality-optimal solutions, for example maximum satisfiability (MaxSAT) or weak constraints in Answer Set Programming (ASP). Clearly each cardinality-optimal solution is also a subset-optimal one, and if the language also allows for the addition of particular restricting constructs (both MaxSAT and ASP do) then all subset-optimal solutions can be found by an iterative computation of cardinality-optimal solutions. As a showcase, the computation of preferred extensions of abstract argumentation frameworks using the proposed method is studied.

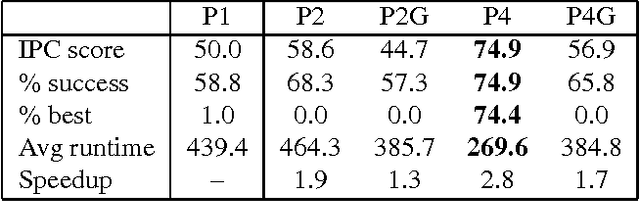
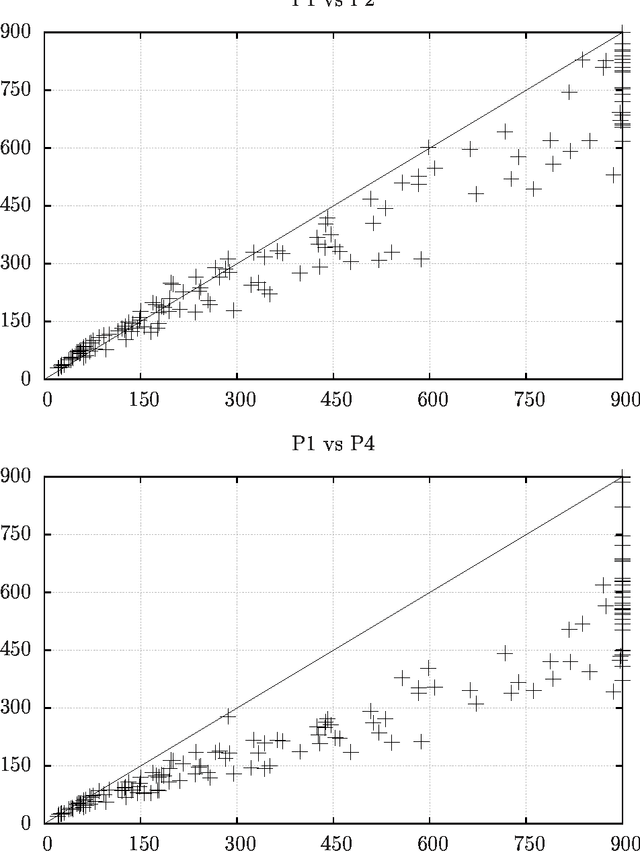
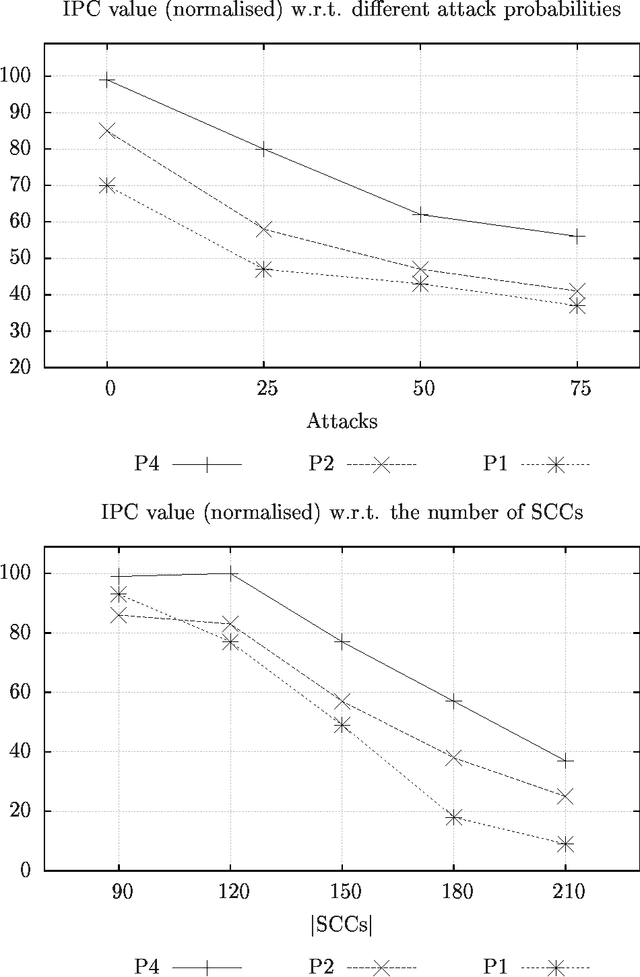
Exploiting Parallelism for Hard Problems in Abstract Argumentation: Technical Report

Abstract argumentation framework (\AFname) is a unifying framework able to encompass a variety of nonmonotonic reasoning approaches, logic programming and computational argumentation. Yet, efficient approaches for most of the decision and enumeration problems associated to \AFname s are missing, thus potentially limiting the efficacy of argumentation-based approaches in real domains. In this paper, we present an algorithm for enumerating the preferred extensions of abstract argumentation frameworks which exploits parallel computation. To this purpose, the SCC-recursive semantics definition schema is adopted, where extensions are defined at the level of specific sub-frameworks. The algorithm shows significant performance improvements in large frameworks, in terms of number of solutions found and speedup.

Computing Preferred Extensions in Abstract Argumentation: a SAT-based Approach

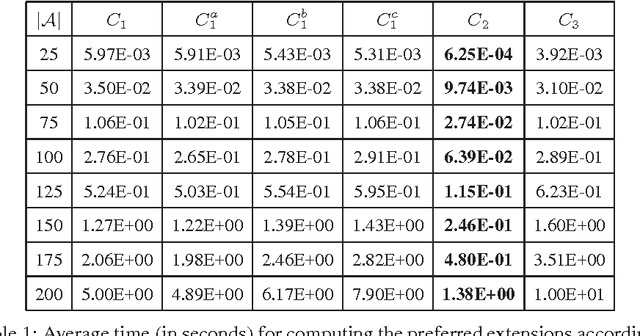
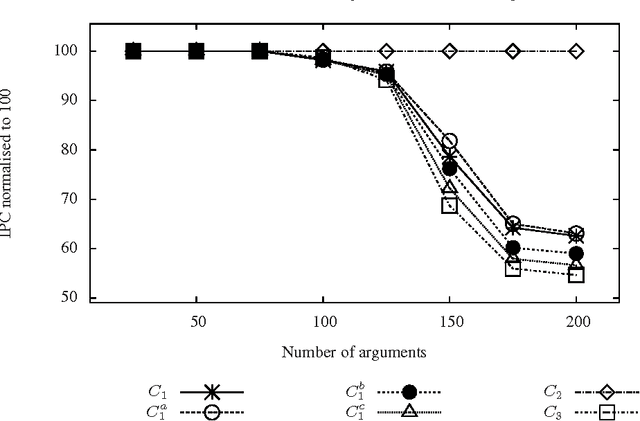
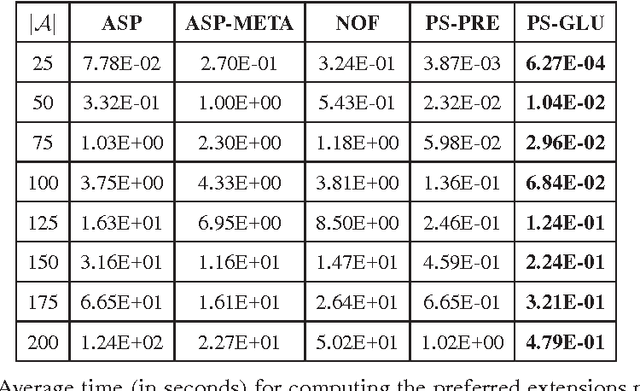
This paper presents a novel SAT-based approach for the computation of extensions in abstract argumentation, with focus on preferred semantics, and an empirical evaluation of its performances. The approach is based on the idea of reducing the problem of computing complete extensions to a SAT problem and then using a depth-first search method to derive preferred extensions. The proposed approach has been tested using two distinct SAT solvers and compared with three state-of-the-art systems for preferred extension computation. It turns out that the proposed approach delivers significantly better performances in the large majority of the considered cases.