Automata for Infinite Argumentation Structures

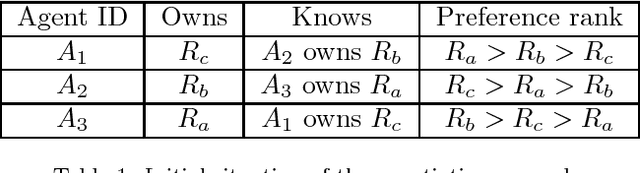
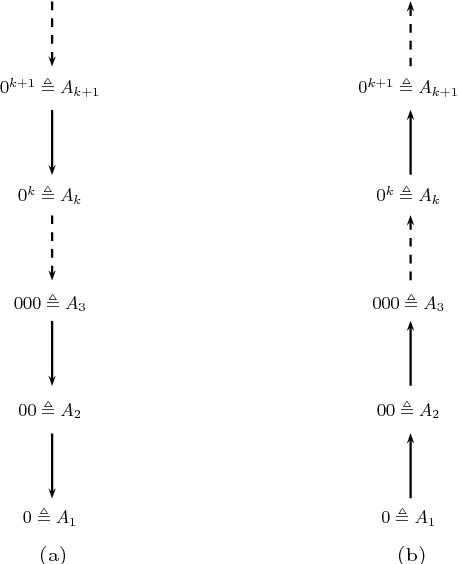
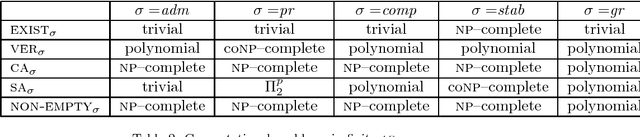
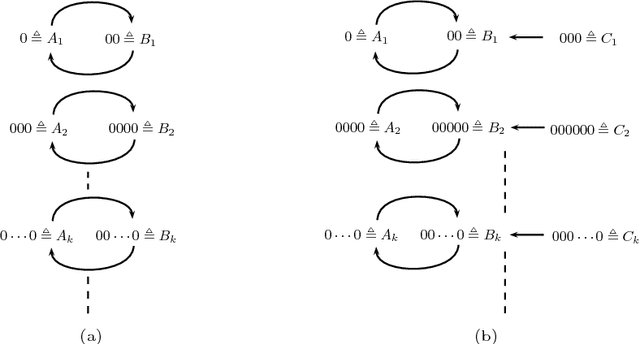
The theory of abstract argumentation frameworks (afs) has, in the main, focused on finite structures, though there are many significant contexts where argumentation can be regarded as a process involving infinite objects. To address this limitation, in this paper we propose a novel approach for describing infinite afs using tools from formal language theory. In particular, the possibly infinite set of arguments is specified through the language recognized by a deterministic finite automaton while a suitable formalism, called attack expression, is introduced to describe the relation of attack between arguments. The proposed approach is shown to satisfy some desirable properties which can not be achieved through other "naive" uses of formal languages. In particular, the approach is shown to be expressive enough to capture (besides any arbitrary finite structure) a large variety of infinite afs including two major examples from previous literature and two sample cases from the domains of multi-agent negotiation and ambient intelligence. On the computational side, we show that several decision and construction problems which are known to be polynomial time solvable in finite afs are decidable in the context of the proposed formalism and we provide the relevant algorithms. Moreover we obtain additional results concerning the case of finitary afs.

Computing Preferred Extensions in Abstract Argumentation: a SAT-based Approach

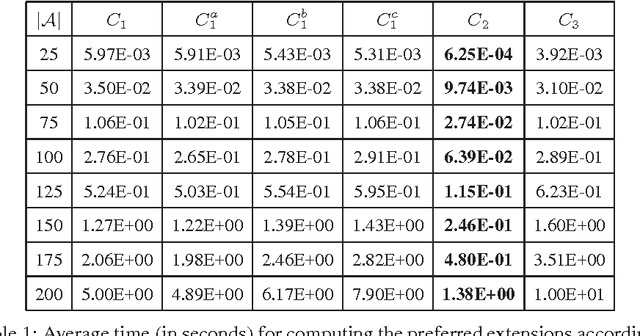
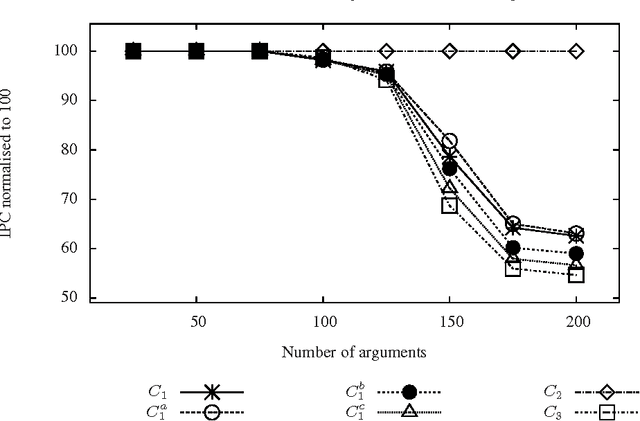
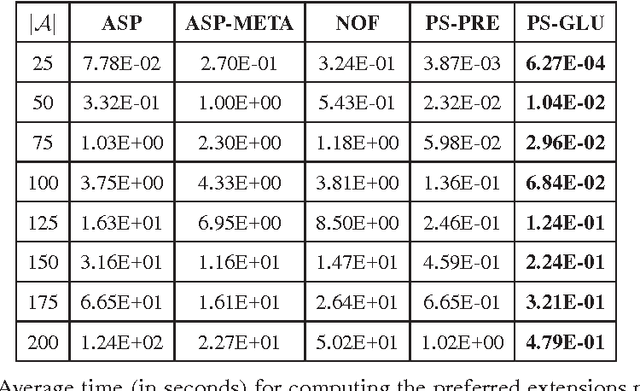
This paper presents a novel SAT-based approach for the computation of extensions in abstract argumentation, with focus on preferred semantics, and an empirical evaluation of its performances. The approach is based on the idea of reducing the problem of computing complete extensions to a SAT problem and then using a depth-first search method to derive preferred extensions. The proposed approach has been tested using two distinct SAT solvers and compared with three state-of-the-art systems for preferred extension computation. It turns out that the proposed approach delivers significantly better performances in the large majority of the considered cases.

On Concise Encodings of Preferred Extensions

Much work on argument systems has focussed on preferred extensions which define the maximal collectively defensible subsets. Identification and enumeration of these subsets is (under the usual assumptions) computationally demanding. We consider approaches to deciding if a subset S is a preferred extension which query a representations encoding all such extensions, so that the computational effort is invested once only (for the initial enumeration) rather than for each separate query.