Reinforcement Learning to Disentangle Multiqubit Quantum States from Partial Observations

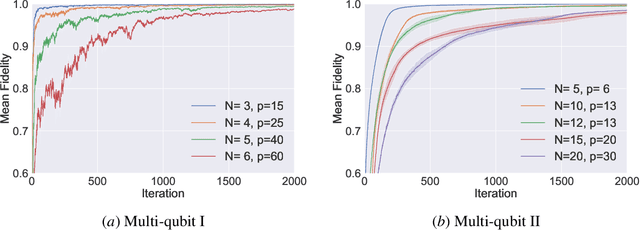
Using partial knowledge of a quantum state to control multiqubit entanglement is a largely unexplored paradigm in the emerging field of quantum interactive dynamics with the potential to address outstanding challenges in quantum state preparation and compression, quantum control, and quantum complexity. We present a deep reinforcement learning (RL) approach to constructing short disentangling circuits for arbitrary 4-, 5-, and 6-qubit states using an actor-critic algorithm. With access to only two-qubit reduced density matrices, our agent decides which pairs of qubits to apply two-qubit gates on; requiring only local information makes it directly applicable on modern NISQ devices. Utilizing a permutation-equivariant transformer architecture, the agent can autonomously identify qubit permutations within the state, and adjusts the disentangling protocol accordingly. Once trained, it provides circuits from different initial states without further optimization. We demonstrate the agent's ability to identify and exploit the entanglement structure of multiqubit states. For 4-, 5-, and 6-qubit Haar-random states, the agent learns to construct disentangling circuits that exhibit strong correlations both between consecutive gates and among the qubits involved. Through extensive benchmarking, we show the efficacy of the RL approach to find disentangling protocols with minimal gate resources. We explore the resilience of our trained agents to noise, highlighting their potential for real-world quantum computing applications. Analyzing optimal disentangling protocols, we report a general circuit to prepare an arbitrary 4-qubit state using at most 5 two-qubit (10 CNOT) gates.

Monte Carlo Tree Search based Hybrid Optimization of Variational Quantum Circuits

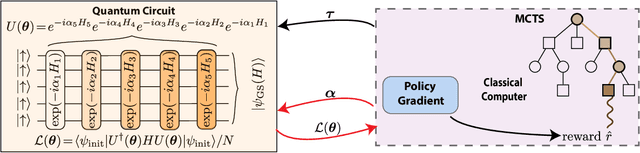
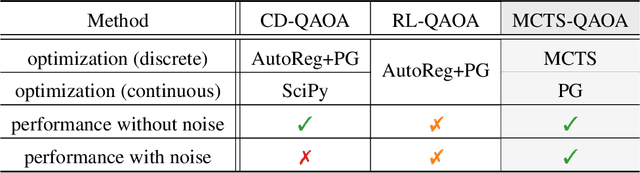
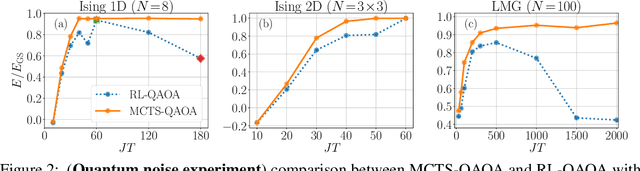
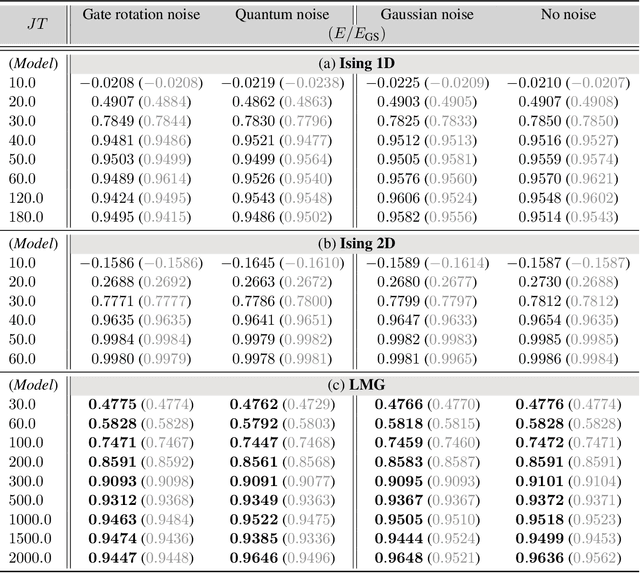
Variational quantum algorithms stand at the forefront of simulations on near-term and future fault-tolerant quantum devices. While most variational quantum algorithms involve only continuous optimization variables, the representational power of the variational ansatz can sometimes be significantly enhanced by adding certain discrete optimization variables, as is exemplified by the generalized quantum approximate optimization algorithm (QAOA). However, the hybrid discrete-continuous optimization problem in the generalized QAOA poses a challenge to the optimization. We propose a new algorithm called MCTS-QAOA, which combines a Monte Carlo tree search method with an improved natural policy gradient solver to optimize the discrete and continuous variables in the quantum circuit, respectively. We find that MCTS-QAOA has excellent noise-resilience properties and outperforms prior algorithms in challenging instances of the generalized QAOA.

Noise-Robust End-to-End Quantum Control using Deep Autoregressive Policy Networks

Variational quantum eigensolvers have recently received increased attention, as they enable the use of quantum computing devices to find solutions to complex problems, such as the ground energy and ground state of strongly-correlated quantum many-body systems. In many applications, it is the optimization of both continuous and discrete parameters that poses a formidable challenge. Using reinforcement learning (RL), we present a hybrid policy gradient algorithm capable of simultaneously optimizing continuous and discrete degrees of freedom in an uncertainty-resilient way. The hybrid policy is modeled by a deep autoregressive neural network to capture causality. We employ the algorithm to prepare the ground state of the nonintegrable quantum Ising model in a unitary process, parametrized by a generalized quantum approximate optimization ansatz: the RL agent solves the discrete combinatorial problem of constructing the optimal sequences of unitaries out of a predefined set and, at the same time, it optimizes the continuous durations for which these unitaries are applied. We demonstrate the noise-robust features of the agent by considering three sources of uncertainty: classical and quantum measurement noise, and errors in the control unitary durations. Our work exhibits the beneficial synergy between reinforcement learning and quantum control.

Reinforcement Learning for Many-Body Ground State Preparation based on Counter-Diabatic Driving

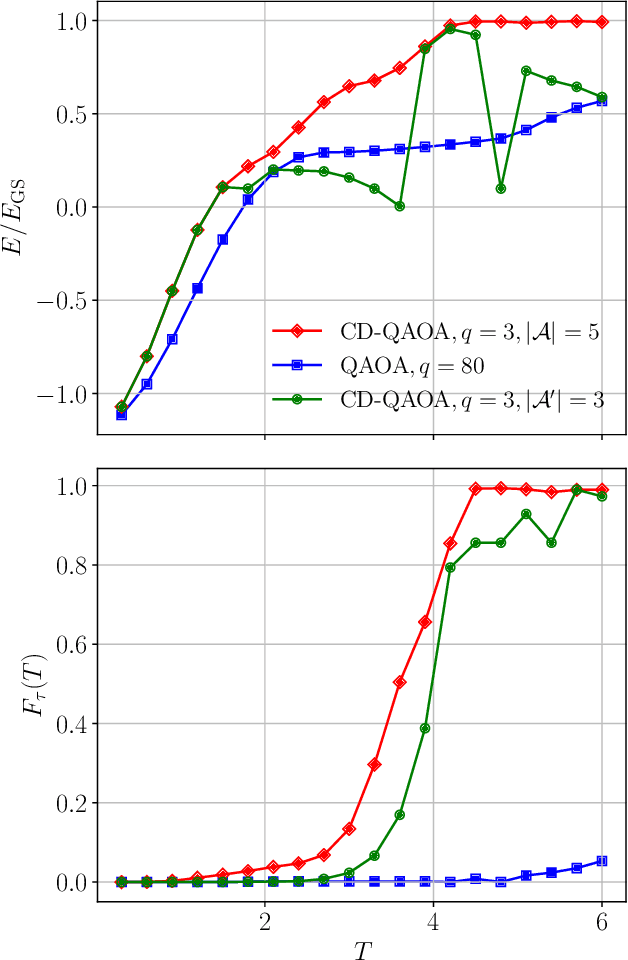
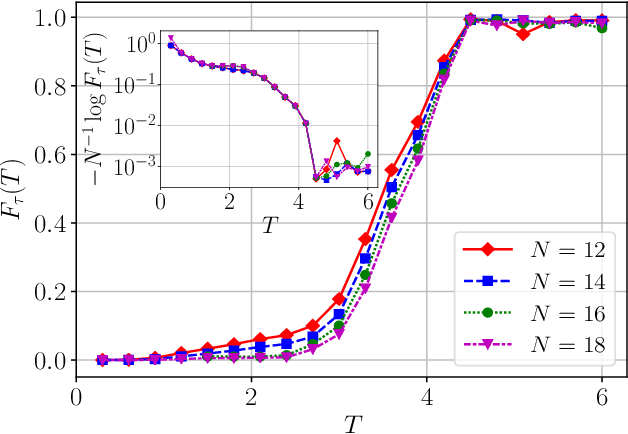
The Quantum Approximate Optimization Ansatz (QAOA) is a prominent example of variational quantum algorithms. We propose a generalized QAOA ansatz called CD-QAOA, which is inspired by the counter-diabatic (CD) driving procedure, designed for quantum many-body systems, and optimized using a reinforcement learning (RL) approach. The resulting hybrid control algorithm proves versatile in preparing the ground state of quantum-chaotic many-body spin chains, by minimizing the energy. We show that using terms occurring in the adiabatic gauge potential as additional control unitaries, it is possible to achieve fast high-fidelity many-body control away from the adiabatic regime. While each unitary retains the conventional QAOA-intrinsic continuous control degree of freedom such as the time duration, we take into account the order of the multiple available unitaries appearing in the control sequence as an additional discrete optimization problem. Endowing the policy gradient algorithm with an autoregressive deep learning architecture to capture causality, we train the RL agent to construct optimal sequences of unitaries. The algorithm has no access to the quantum state, and we find that the protocol learned on small systems may generalize to larger systems. By scanning a range of protocol durations, we present numerical evidence for a finite quantum speed limit in the nonintegrable mixed-field spin-1/2 Ising model, and for the suitability of the ansatz to prepare ground states of the spin-1 Heisenberg chain in the long-range and topologically ordered parameter regimes. This work paves the way to incorporate recent success from deep learning for the purpose of quantum many-body control.

Policy Gradient based Quantum Approximate Optimization Algorithm

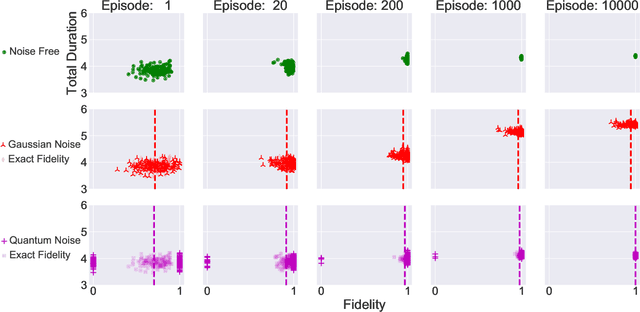
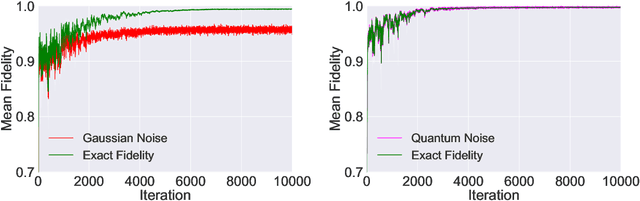
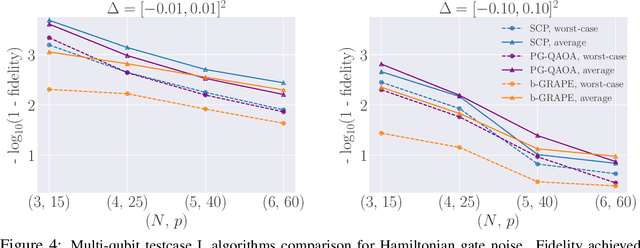
The quantum approximate optimization algorithm (QAOA), as a hybrid quantum/classical algorithm, has received much interest recently. QAOA can also be viewed as a variational ansatz for quantum control. However, its direct application to emergent quantum technology encounters additional physical constraints: (i) the states of the quantum system are not observable; (ii) obtaining the derivatives of the objective function can be computationally expensive or even inaccessible in experiments, and (iii) the values of the objective function may be sensitive to various sources of uncertainty, as is the case for noisy intermediate-scale quantum (NISQ) devices. Taking such constraints into account, we show that policy-gradient-based reinforcement learning (RL) algorithms are well suited for optimizing the variational parameters of QAOA in a noise-robust fashion, opening up the way for developing RL techniques for continuous quantum control. This is advantageous to help mitigate and monitor the potentially unknown sources of errors in modern quantum simulators. We analyze the performance of the algorithm for quantum state transfer problems in single- and multi-qubit systems, subject to various sources of noise such as error terms in the Hamiltonian, or quantum uncertainty in the measurement process. We show that, in noisy setups, it is capable of outperforming state-of-the-art existing optimization algorithms.

A high-bias, low-variance introduction to Machine Learning for physicists

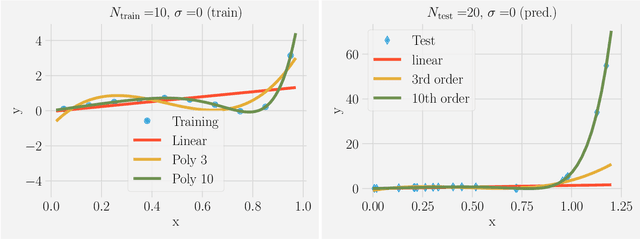
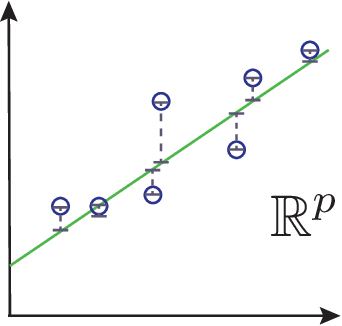
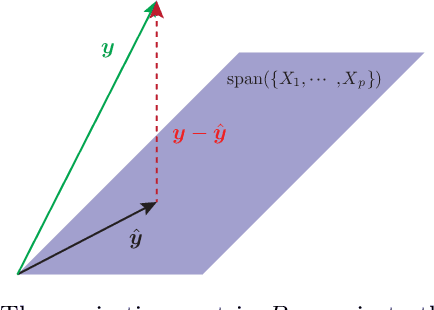
Machine Learning (ML) is one of the most exciting and dynamic areas of modern research and application. The purpose of this review is to provide an introduction to the core concepts and tools of machine learning in a manner easily understood and intuitive to physicists. The review begins by covering fundamental concepts in ML and modern statistics such as the bias-variance tradeoff, overfitting, regularization, and generalization before moving on to more advanced topics in both supervised and unsupervised learning. Topics covered in the review include ensemble models, deep learning and neural networks, clustering and data visualization, energy-based models (including MaxEnt models and Restricted Boltzmann Machines), and variational methods. Throughout, we emphasize the many natural connections between ML and statistical physics. A notable aspect of the review is the use of Python notebooks to introduce modern ML/statistical packages to readers using physics-inspired datasets (the Ising Model and Monte-Carlo simulations of supersymmetric decays of proton-proton collisions). We conclude with an extended outlook discussing possible uses of machine learning for furthering our understanding of the physical world as well as open problems in ML where physicists maybe able to contribute. (Notebooks are available at https://physics.bu.edu/~pankajm/MLnotebooks.html )