A note on spike localization for line spectrum estimation

This note considers the problem of approximating the locations of dominant spikes for a probability measure from noisy spectrum measurements under the condition of residue signal, significant noise level, and no minimum spectrum separation. We show that the simple procedure of thresholding the smoothed inverse Fourier transform allows for approximating the spike locations rather accurately.

Monte Carlo Tree Search based Hybrid Optimization of Variational Quantum Circuits

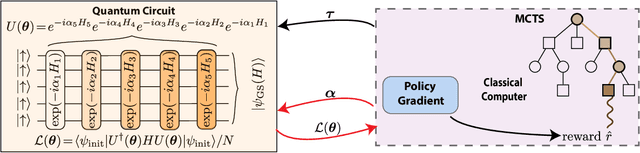
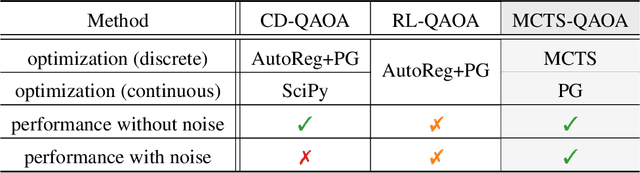
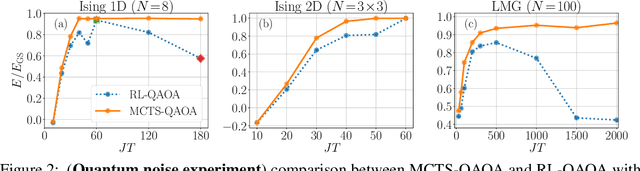
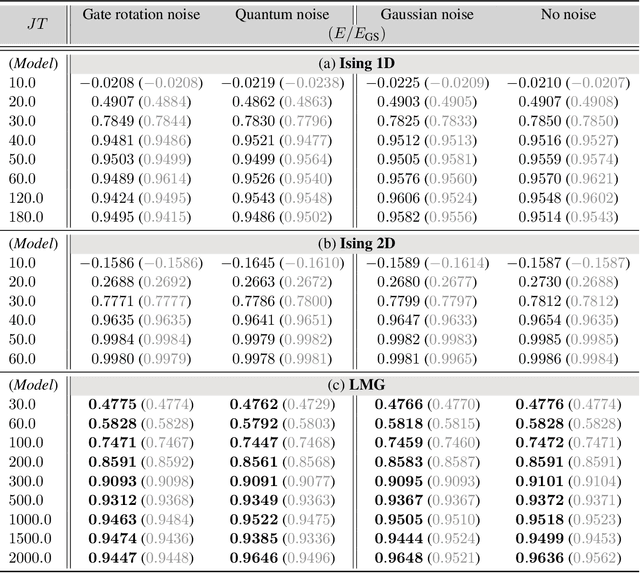
Variational quantum algorithms stand at the forefront of simulations on near-term and future fault-tolerant quantum devices. While most variational quantum algorithms involve only continuous optimization variables, the representational power of the variational ansatz can sometimes be significantly enhanced by adding certain discrete optimization variables, as is exemplified by the generalized quantum approximate optimization algorithm (QAOA). However, the hybrid discrete-continuous optimization problem in the generalized QAOA poses a challenge to the optimization. We propose a new algorithm called MCTS-QAOA, which combines a Monte Carlo tree search method with an improved natural policy gradient solver to optimize the discrete and continuous variables in the quantum circuit, respectively. We find that MCTS-QAOA has excellent noise-resilience properties and outperforms prior algorithms in challenging instances of the generalized QAOA.

Accelerating Primal-dual Methods for Regularized Markov Decision Processes

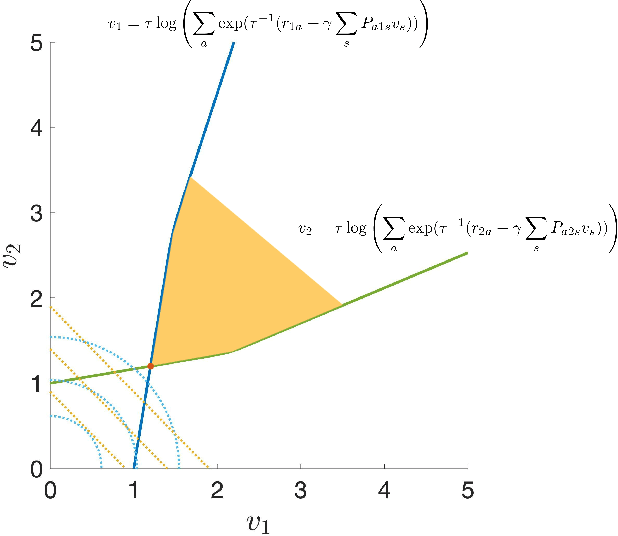
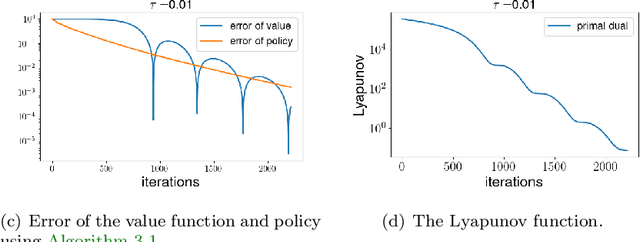
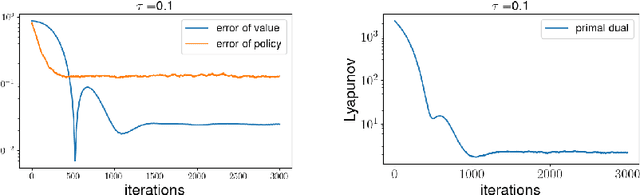
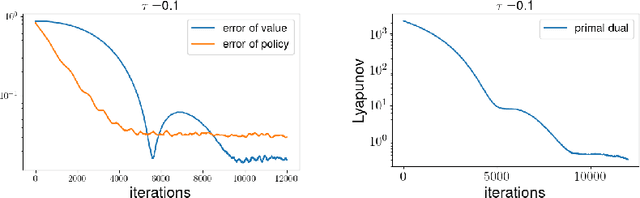
Entropy regularized Markov decision processes have been widely used in reinforcement learning. This paper is concerned with the primal-dual formulation of the entropy regularized problems. Standard first-order methods suffer from slow convergence due to the lack of strict convexity and concavity. To address this issue, we first introduce a new quadratically convexified primal-dual formulation. The natural gradient ascent descent of the new formulation enjoys global convergence guarantee and exponential convergence rate. We also propose a new interpolating metric that further accelerates the convergence significantly. Numerical results are provided to demonstrate the performance of the proposed methods under multiple settings.

Quasi-Newton policy gradient algorithms

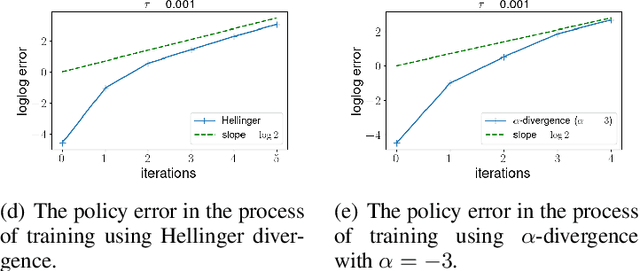
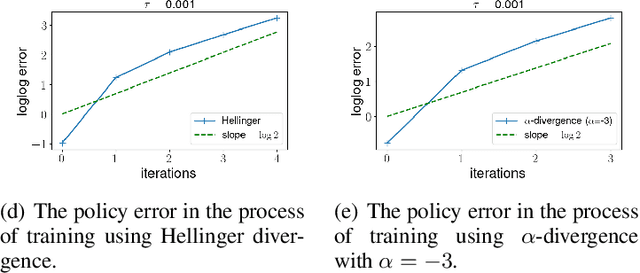
Policy gradient algorithms have been widely applied to reinforcement learning (RL) problems in recent years. Regularization with various entropy functions is often used to encourage exploration and improve stability. In this paper, we propose a quasi-Newton method for the policy gradient algorithm with entropy regularization. In the case of Shannon entropy, the resulting algorithm reproduces the natural policy gradient (NPG) algorithm. For other entropy functions, this method results in brand new policy gradient algorithms. We provide a simple proof that all these algorithms enjoy the Newton-type quadratic convergence near the optimal policy. Using synthetic and industrial-scale examples, we demonstrate that the proposed quasi-Newton method typically converges in single-digit iterations, often orders of magnitude faster than other state-of-the-art algorithms.

A semigroup method for high dimensional elliptic PDEs and eigenvalue problems based on neural networks

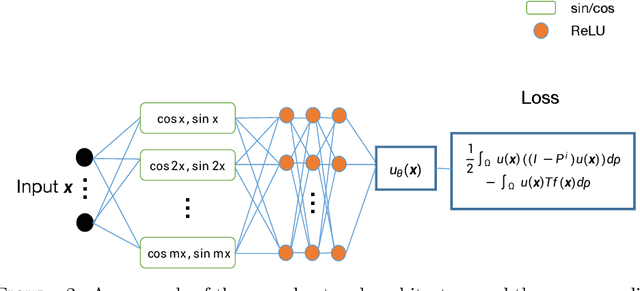
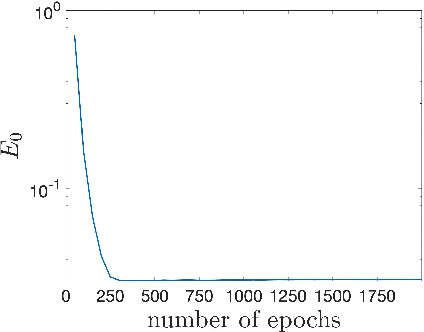
In this paper, we propose a semigroup method for solving high-dimensional elliptic partial differential equations (PDEs) and the associated eigenvalue problems based on neural networks. For the PDE problems, we reformulate the original equations as variational problems with the help of semigroup operators and then solve the variational problems with neural network (NN) parameterization. The main advantages are that no mixed second-order derivative computation is needed during the stochastic gradient descent training and that the boundary conditions are taken into account automatically by the semigroup operator. For eigenvalue problems, a primal-dual method is proposed, resolving the constraint with a scalar dual variable. Numerical results are provided to demonstrate the performance of the proposed methods.

Solving for high dimensional committor functions using neural network with online approximation to derivatives

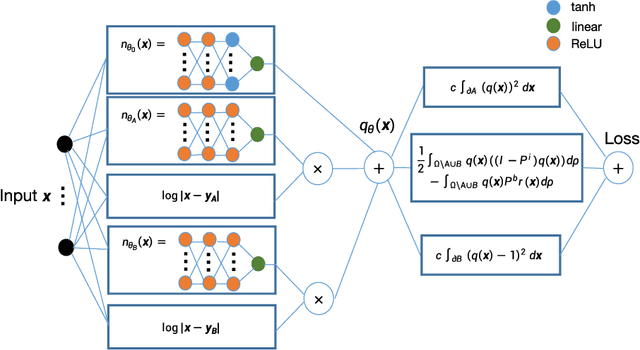
This paper proposes a new method based on neural networks for computing the high-dimensional committor functions that satisfy Fokker-Planck equations. Instead of working with partial differential equations, the new method works with an integral formulation that involves the semigroup of the differential operator. The variational form of the new formulation is then solved by parameterizing the committor function as a neural network. As the main benefit of this new approach, stochastic gradient descent type algorithms can be applied in the training of the committor function without the need of computing any second-order derivatives. Numerical results are provided to demonstrate the performance of the proposed method.