GiNGR: Generalized Iterative Non-Rigid Point Cloud and Surface Registration Using Gaussian Process Regression

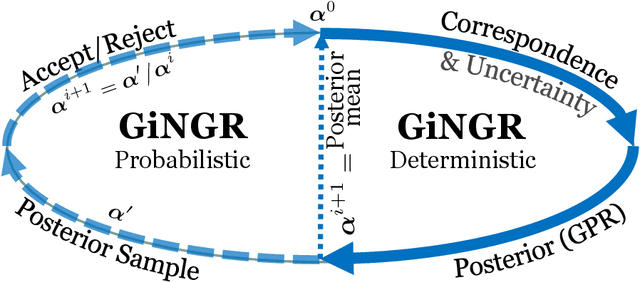
In this paper, we unify popular non-rigid registration methods for point sets and surfaces under our general framework, GiNGR. GiNGR builds upon Gaussian Process Morphable Models (GPMM) and hence separates modeling the deformation prior from model adaptation for registration. In addition, it provides explainable hyperparameters, multi-resolution registration, trivial inclusion of expert annotation, and the ability to use and combine analytical and statistical deformation priors. But more importantly, the reformulation allows for a direct comparison of registration methods. Instead of using a general solver in the optimization step, we show how Gaussian process regression (GPR) iteratively can warp a reference onto a target, leading to smooth deformations following the prior for any dense, sparse, or partial estimated correspondences in a principled way. We show how the popular CPD and ICP algorithms can be directly explained with GiNGR. Furthermore, we show how existing algorithms in the GiNGR framework can perform probabilistic registration to obtain a distribution of different registrations instead of a single best registration. This can be used to analyze the uncertainty e.g. when registering partial observations. GiNGR is publicly available and fully modular to allow for domain-specific prior construction.

Dynamic multi feature-class Gaussian process models

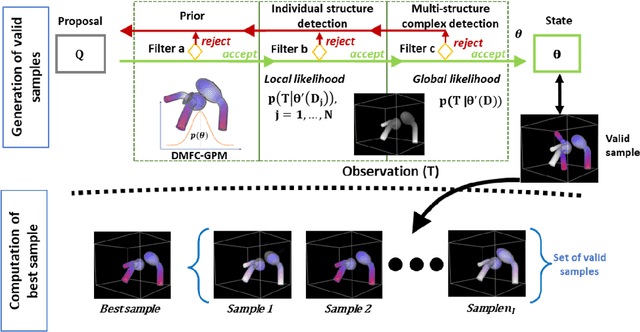
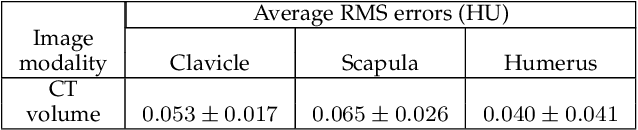
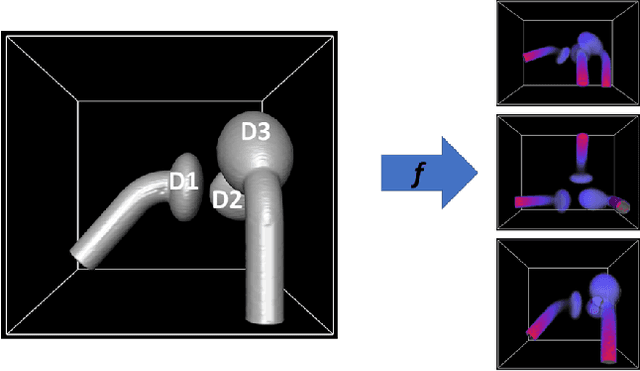
In model-based medical image analysis, three features of interest are the shape of structures of interest, their relative pose, and image intensity profiles representative of some physical property. Often, these are modelled separately through statistical models by decomposing the object's features into a set of basis functions through principal geodesic analysis or principal component analysis. This study presents a statistical modelling method for automatic learning of shape, pose and intensity features in medical images which we call the Dynamic multi feature-class Gaussian process models (DMFC-GPM). A DMFC-GPM is a Gaussian process (GP)-based model with a shared latent space that encodes linear and non-linear variation. Our method is defined in a continuous domain with a principled way to represent shape, pose and intensity feature classes in a linear space, based on deformation fields. A deformation field-based metric is adapted in the method for modelling shape and intensity feature variation as well as for comparing rigid transformations (pose). Moreover, DMFC-GPMs inherit properties intrinsic to GPs including marginalisation and regression. Furthermore, they allow for adding additional pose feature variability on top of those obtained from the image acquisition process; what we term as permutation modelling. For image analysis tasks using DMFC-GPMs, we adapt Metropolis-Hastings algorithms making the prediction of features fully probabilistic. We validate the method using controlled synthetic data and we perform experiments on bone structures from CT images of the shoulder to illustrate the efficacy of the model for pose and shape feature prediction. The model performance results suggest that this new modelling paradigm is robust, accurate, accessible, and has potential applications including the management of musculoskeletal disorders and clinical decision making

A Closest Point Proposal for MCMC-based Probabilistic Surface Registration

In this paper, we propose a non-rigid surface registration algorithm that estimates the correspondence uncertainty using the Markov-chain Monte Carlo (MCMC) framework. The estimated uncertainty of the inferred registration is important for many applications, such as surgical planning or missing data reconstruction. The used Metropolis-Hastings (MH) algorithm decouples the inference from modelling the posterior using a propose-and-verify scheme. The widely used random sampling strategy leads to slow convergence rates in high dimensional space. In order to overcome this limitation, we introduce an informed probabilistic proposal based on ICP that can be used within the MH algorithm. While the ICP algorithm is used in the inference algorithm, the likelihood can be chosen independently. We showcase different surface distance measures, such as the traditional Euclidean norm and the Hausdorff distance. While quantifying the uncertainty of the correspondence, we also experimentally verify that our method is more robust than the non-rigid ICP algorithm and provides more accurate surface registrations. In a reconstruction task, we show how our probabilistic framework can be used to estimate the posterior distribution of missing data without assuming a fixed point-to-point correspondence. We have made our registration framework publicly available for the community.

Morphable Face Models - An Open Framework

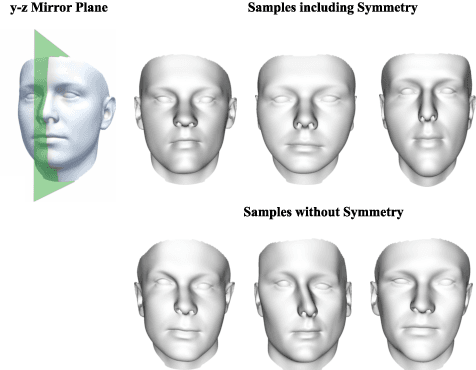
In this paper, we present a novel open-source pipeline for face registration based on Gaussian processes as well as an application to face image analysis. Non-rigid registration of faces is significant for many applications in computer vision, such as the construction of 3D Morphable face models (3DMMs). Gaussian Process Morphable Models (GPMMs) unify a variety of non-rigid deformation models with B-splines and PCA models as examples. GPMM separate problem specific requirements from the registration algorithm by incorporating domain-specific adaptions as a prior model. The novelties of this paper are the following: (i) We present a strategy and modeling technique for face registration that considers symmetry, multi-scale and spatially-varying details. The registration is applied to neutral faces and facial expressions. (ii) We release an open-source software framework for registration and model-building, demonstrated on the publicly available BU3D-FE database. The released pipeline also contains an implementation of an Analysis-by-Synthesis model adaption of 2D face images, tested on the Multi-PIE and LFW database. This enables the community to reproduce, evaluate and compare the individual steps of registration to model-building and 3D/2D model fitting. (iii) Along with the framework release, we publish a new version of the Basel Face Model (BFM-2017) with an improved age distribution and an additional facial expression model.

Gaussian Process Morphable Models

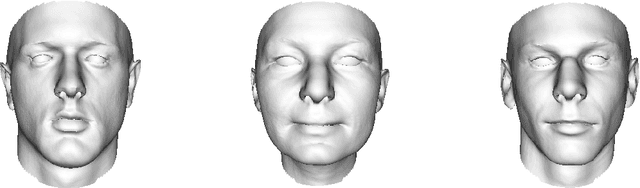
Statistical shape models (SSMs) represent a class of shapes as a normal distribution of point variations, whose parameters are estimated from example shapes. Principal component analysis (PCA) is applied to obtain a low-dimensional representation of the shape variation in terms of the leading principal components. In this paper, we propose a generalization of SSMs, called Gaussian Process Morphable Models (GPMMs). We model the shape variations with a Gaussian process, which we represent using the leading components of its Karhunen-Loeve expansion. To compute the expansion, we make use of an approximation scheme based on the Nystrom method. The resulting model can be seen as a continuous analogon of an SSM. However, while for SSMs the shape variation is restricted to the span of the example data, with GPMMs we can define the shape variation using any Gaussian process. For example, we can build shape models that correspond to classical spline models, and thus do not require any example data. Furthermore, Gaussian processes make it possible to combine different models. For example, an SSM can be extended with a spline model, to obtain a model that incorporates learned shape characteristics, but is flexible enough to explain shapes that cannot be represented by the SSM. We introduce a simple algorithm for fitting a GPMM to a surface or image. This results in a non-rigid registration approach, whose regularization properties are defined by a GPMM. We show how we can obtain different registration schemes,including methods for multi-scale, spatially-varying or hybrid registration, by constructing an appropriate GPMM. As our approach strictly separates modelling from the fitting process, this is all achieved without changes to the fitting algorithm. We show the applicability and versatility of GPMMs on a clinical use case, where the goal is the model-based segmentation of 3D forearm images.