Injective Flows for parametric hypersurfaces

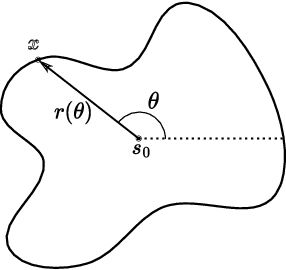
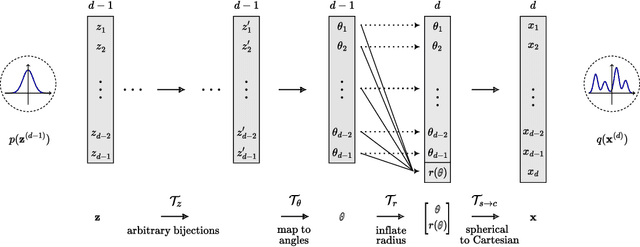
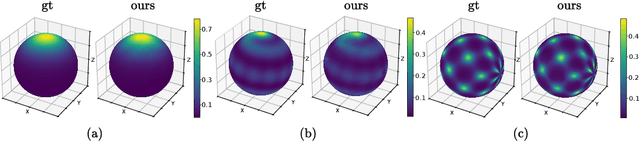
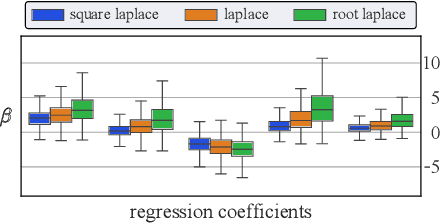
Normalizing Flows (NFs) are powerful and efficient models for density estimation. When modeling densities on manifolds, NFs can be generalized to injective flows but the Jacobian determinant becomes computationally prohibitive. Current approaches either consider bounds on the log-likelihood or rely on some approximations of the Jacobian determinant. In contrast, we propose injective flows for parametric hypersurfaces and show that for such manifolds we can compute the Jacobian determinant exactly and efficiently, with the same cost as NFs. Furthermore, we show that for the subclass of star-like manifolds we can extend the proposed framework to always allow for a Cartesian representation of the density. We showcase the relevance of modeling densities on hypersurfaces in two settings. Firstly, we introduce a novel Objective Bayesian approach to penalized likelihood models by interpreting level-sets of the penalty as star-like manifolds. Secondly, we consider Bayesian mixture models and introduce a general method for variational inference by defining the posterior of mixture weights on the probability simplex.

Lagrangian Flow Networks for Conservation Laws

We introduce Lagrangian Flow Networks (LFlows) for modeling fluid densities and velocities continuously in space and time. The proposed LFlows satisfy by construction the continuity equation, a PDE describing mass conservation in its differentiable form. Our model is based on the insight that solutions to the continuity equation can be expressed as time-dependent density transformations via differentiable and invertible maps. This follows from classical theory of existence and uniqueness of Lagrangian flows for smooth vector fields. Hence, we model fluid densities by transforming a base density with parameterized diffeomorphisms conditioned on time. The key benefit compared to methods relying on Neural-ODE or PINNs is that the analytic expression of the velocity is always consistent with the density. Furthermore, there is no need for expensive numerical solvers, nor for enforcing the PDE with penalty methods. Lagrangian Flow Networks show improved predictive accuracy on synthetic density modeling tasks compared to competing models in both 2D and 3D. We conclude with a real-world application of modeling bird migration based on sparse weather radar measurements.

GiNGR: Generalized Iterative Non-Rigid Point Cloud and Surface Registration Using Gaussian Process Regression

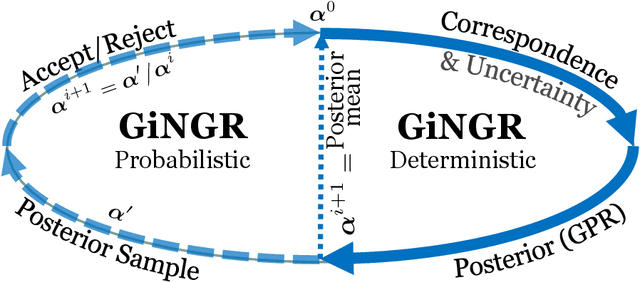
In this paper, we unify popular non-rigid registration methods for point sets and surfaces under our general framework, GiNGR. GiNGR builds upon Gaussian Process Morphable Models (GPMM) and hence separates modeling the deformation prior from model adaptation for registration. In addition, it provides explainable hyperparameters, multi-resolution registration, trivial inclusion of expert annotation, and the ability to use and combine analytical and statistical deformation priors. But more importantly, the reformulation allows for a direct comparison of registration methods. Instead of using a general solver in the optimization step, we show how Gaussian process regression (GPR) iteratively can warp a reference onto a target, leading to smooth deformations following the prior for any dense, sparse, or partial estimated correspondences in a principled way. We show how the popular CPD and ICP algorithms can be directly explained with GiNGR. Furthermore, we show how existing algorithms in the GiNGR framework can perform probabilistic registration to obtain a distribution of different registrations instead of a single best registration. This can be used to analyze the uncertainty e.g. when registering partial observations. GiNGR is publicly available and fully modular to allow for domain-specific prior construction.