"What" x "When" working memory representations using Laplace Neural Manifolds

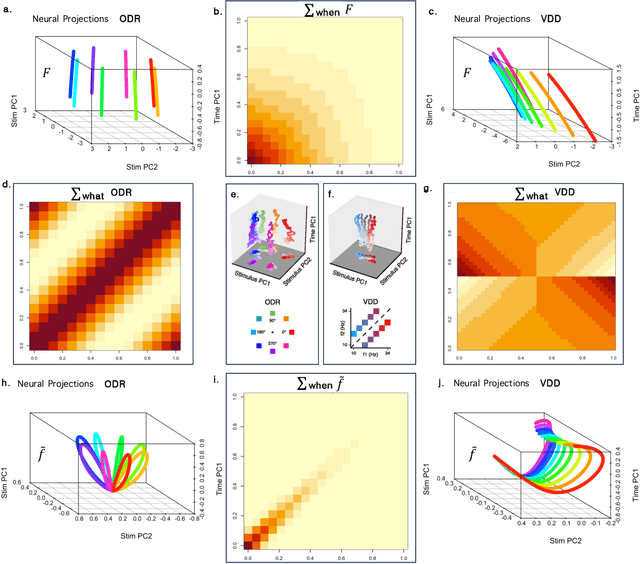
Working memory $\unicode{x2013}$ the ability to remember recent events as they recede continuously into the past $\unicode{x2013}$ requires the ability to represent any stimulus at any time delay. This property requires neurons coding working memory to show mixed selectivity, with conjunctive receptive fields (RFs) for stimuli and time, forming a representation of 'what' $\times$ 'when'. We study the properties of such a working memory in simple experiments where a single stimulus must be remembered for a short time. The requirement of conjunctive receptive fields allows the covariance matrix of the network to decouple neatly, allowing an understanding of the low-dimensional dynamics of the population. Different choices of temporal basis functions lead to qualitatively different dynamics. We study a specific choice $\unicode{x2013}$ a Laplace space with exponential basis functions for time coupled to an "Inverse Laplace" space with circumscribed basis functions in time. We refer to this choice with basis functions that evenly tile log time as a Laplace Neural Manifold. Despite the fact that they are related to one another by a linear projection, the Laplace population shows a stable stimulus-specific subspace whereas the Inverse Laplace population shows rotational dynamics. The growth of the rank of the covariance matrix with time depends on the density of the temporal basis set; logarithmic tiling shows good agreement with data. We sketch a continuous attractor CANN that constructs a Laplace Neural Manifold. The attractor in the Laplace space appears as an edge; the attractor for the inverse space appears as a bump. This work provides a map for going from more abstract cognitive models of WM to circuit-level implementation using continuous attractor neural networks, and places constraints on the types of neural dynamics that support working memory.

SITHCon: A neural network robust to variations in input scaling on the time dimension

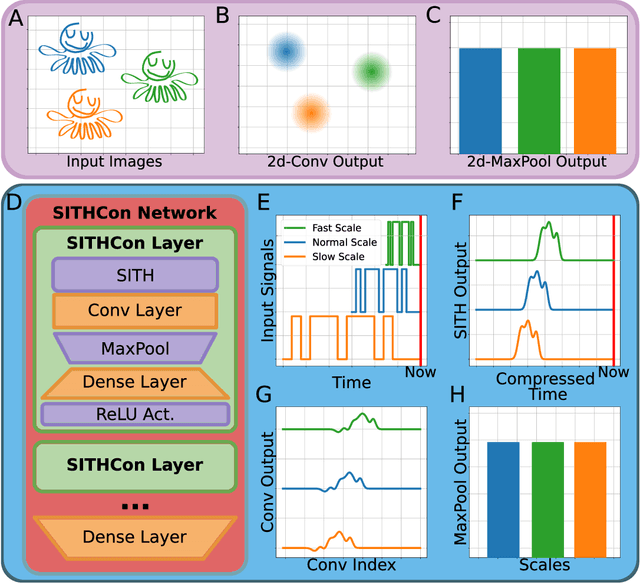
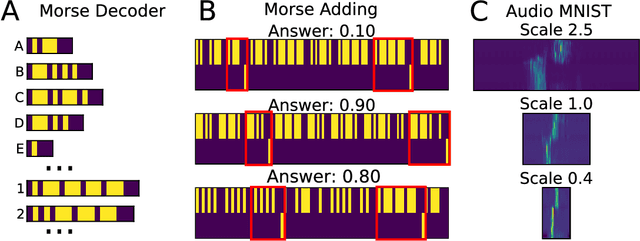
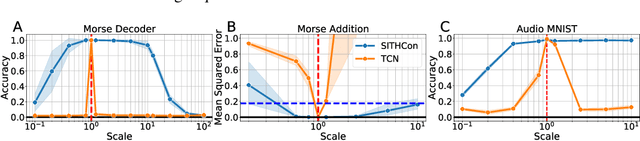
In machine learning, convolutional neural networks (CNNs) have been extremely influential in both computer vision and in recognizing patterns extended over time. In computer vision, part of the flexibility arises from the use of max-pooling operations over the convolutions to attain translation invariance. In the mammalian brain, neural representations of time use a set of temporal basis functions. Critically, these basis functions appear to be arranged in a geometric series such that the basis set is evenly distributed over logarithmic time. This paper introduces a Scale-Invariant Temporal History Convolution network (SITHCon) that uses a logarithmically-distributed temporal memory. A max-pool over a logarithmically-distributed temporal memory results in scale-invariance in time. We compare performance of SITHCon to a Temporal Convolution Network (TCN) and demonstrate that, although both networks can learn classification and regression problems on both univariate and multivariate time series $f(t)$, only SITHCon has the property that it generalizes without retraining to rescaled versions of the input $f(at)$. This property, inspired by findings from neuroscience and psychology, could lead to large-scale networks with dramatically different capabilities, including faster training and greater generalizability, even with significantly fewer free parameters.

DeepSITH: Efficient Learning via Decomposition of What and When Across Time Scales

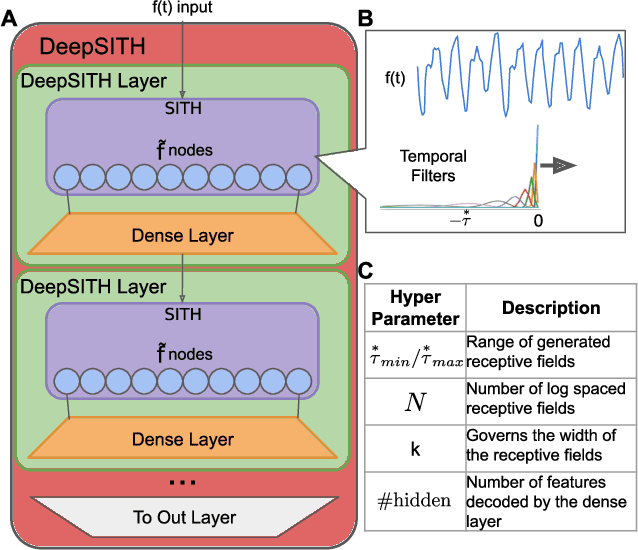
Extracting temporal relationships over a range of scales is a hallmark of human perception and cognition -- and thus it is a critical feature of machine learning applied to real-world problems. Neural networks are either plagued by the exploding/vanishing gradient problem in recurrent neural networks (RNNs) or must adjust their parameters to learn the relevant time scales (e.g., in LSTMs). This paper introduces DeepSITH, a network comprising biologically-inspired Scale-Invariant Temporal History (SITH) modules in series with dense connections between layers. SITH modules respond to their inputs with a geometrically-spaced set of time constants, enabling the DeepSITH network to learn problems along a continuum of time-scales. We compare DeepSITH to LSTMs and other recent RNNs on several time series prediction and decoding tasks. DeepSITH achieves state-of-the-art performance on these problems.

Predicting the future with a scale-invariant temporal memory for the past

In recent years it has become clear that the brain maintains a temporal memory of recent events stretching far into the past. This paper presents a neurally-inspired algorithm to use a scale-invariant temporal representation of the past to predict a scale-invariant future. The result is a scale-invariant estimate of future events as a function of the time at which they are expected to occur. The algorithm is time-local, with credit assigned to the present event by observing how it affects the prediction of the future. To illustrate the potential utility of this approach, we test the model on simultaneous renewal processes with different time scales. The algorithm scales well on these problems despite the fact that the number of states needed to describe them as a Markov process grows exponentially.

Estimating scale-invariant future in continuous time

Natural learners must compute an estimate of future outcomes that follow from a stimulus in continuous time. Widely used reinforcement learning algorithms discretize continuous time and estimate either transition functions from one step to the next (model-based algorithms) or a scalar value of exponentially-discounted future reward using the Bellman equation (model-free algorithms). An important drawback of model-based algorithms is that computational cost grows linearly with the amount of time to be simulated. On the other hand, an important drawback of model-free algorithms is the need to select a time-scale required for exponential discounting. We present a computational mechanism, developed based on work in psychology and neuroscience, for computing a scale-invariant timeline of future outcomes. This mechanism efficiently computes an estimate of inputs as a function of future time on a logarithmically-compressed scale, and can be used to generate a scale-invariant power-law-discounted estimate of expected future reward. The representation of future time retains information about what will happen when. The entire timeline can be constructed in a single parallel operation which generates concrete behavioral and neural predictions. This computational mechanism could be incorporated into future reinforcement learning algorithms.

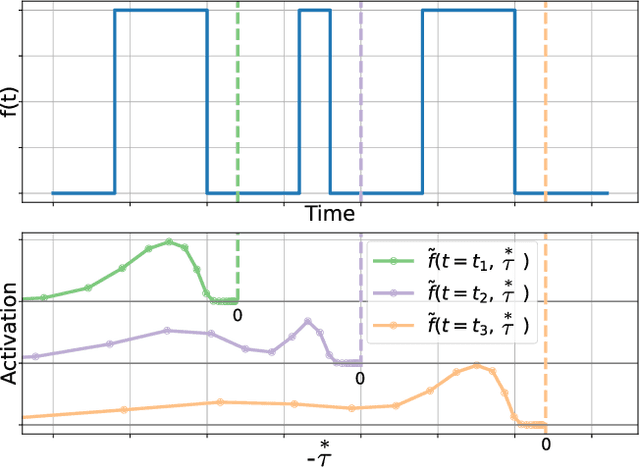
Scale-invariant temporal history (SITH): optimal slicing of the past in an uncertain world

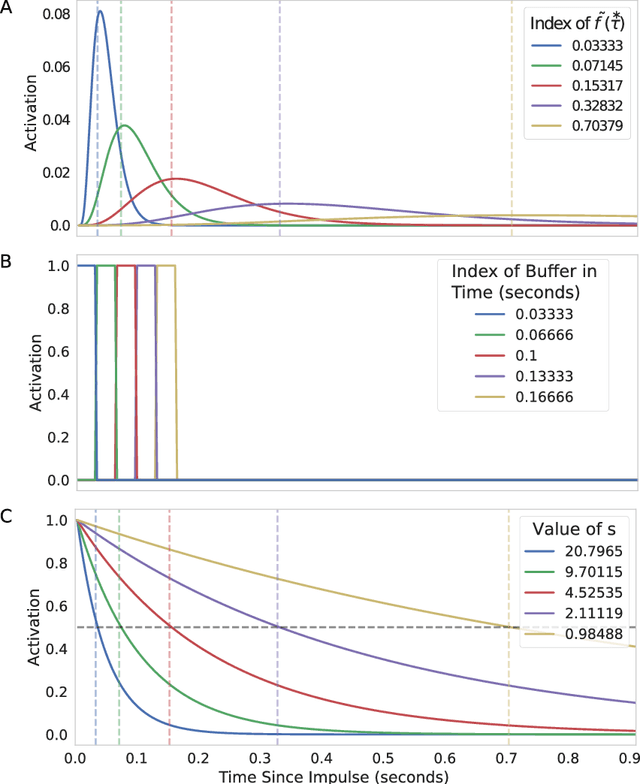
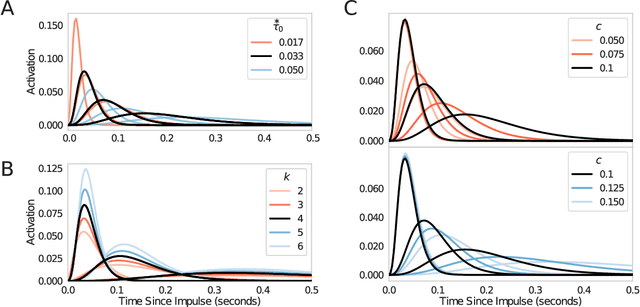
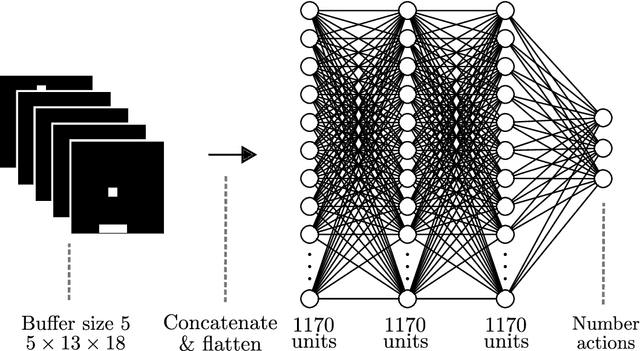
In both the human brain and any general artificial intelligence (AI), a representation of the past is necessary to predict the future. However, perfect storage of all experiences is not feasible. One possibility, utilized in many applications, is to retain information about the past in a buffer. A limitation of this approach is that, although events in the buffer are represented with perfect accuracy, the resources necessary to represent information at multiple time scales go up rapidly. Here we present a neurally-plausible, compressed, scale-free memory representation we call Scale-Invariant Temporal History (SITH). This representation covers an exponentially large period of time at the cost of sacrificing temporal accuracy for events further in the past. The form of this decay is scale-invariant and can be shown to be optimal, in that it is able to respond to worlds with a wide range of relevant time scales. We demonstrate the utility of this representation in learning to play video games at different levels of complexity. In these environments, SITH exhibits better learning performance than both a fixed-size buffer history representation and a representation with exponentially decaying features. Whereas the buffer performs well as long as the temporal dependencies can be represented within the buffer, SITH performs well over a much larger range of time scales with the same amount of resources. Finally, we discuss how the application of SITH, along with other human-inspired models of cognition, could improve reinforcement and machine learning algorithms in general.

Optimally fuzzy temporal memory

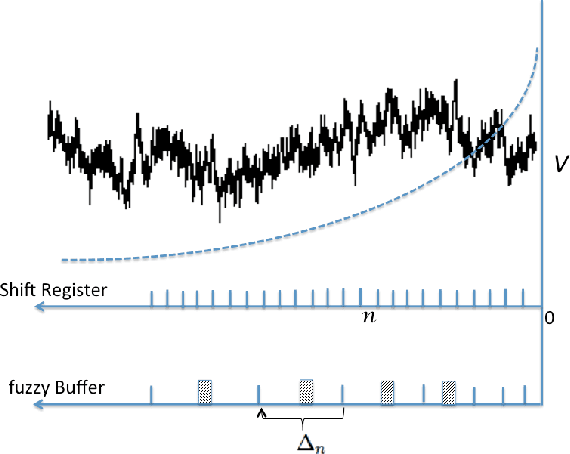
Any learner with the ability to predict the future of a structured time-varying signal must maintain a memory of the recent past. If the signal has a characteristic timescale relevant to future prediction, the memory can be a simple shift register---a moving window extending into the past, requiring storage resources that linearly grows with the timescale to be represented. However, an independent general purpose learner cannot a priori know the characteristic prediction-relevant timescale of the signal. Moreover, many naturally occurring signals show scale-free long range correlations implying that the natural prediction-relevant timescale is essentially unbounded. Hence the learner should maintain information from the longest possible timescale allowed by resource availability. Here we construct a fuzzy memory system that optimally sacrifices the temporal accuracy of information in a scale-free fashion in order to represent prediction-relevant information from exponentially long timescales. Using several illustrative examples, we demonstrate the advantage of the fuzzy memory system over a shift register in time series forecasting of natural signals. When the available storage resources are limited, we suggest that a general purpose learner would be better off committing to such a fuzzy memory system.