SITHCon: A neural network robust to variations in input scaling on the time dimension

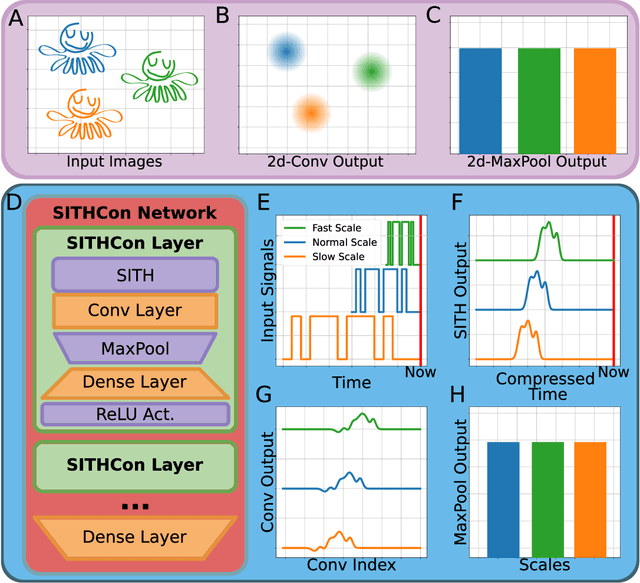
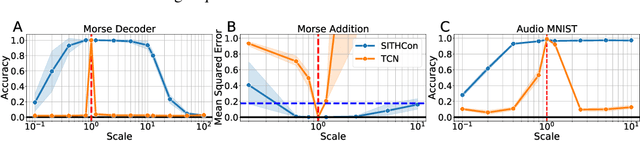
In machine learning, convolutional neural networks (CNNs) have been extremely influential in both computer vision and in recognizing patterns extended over time. In computer vision, part of the flexibility arises from the use of max-pooling operations over the convolutions to attain translation invariance. In the mammalian brain, neural representations of time use a set of temporal basis functions. Critically, these basis functions appear to be arranged in a geometric series such that the basis set is evenly distributed over logarithmic time. This paper introduces a Scale-Invariant Temporal History Convolution network (SITHCon) that uses a logarithmically-distributed temporal memory. A max-pool over a logarithmically-distributed temporal memory results in scale-invariance in time. We compare performance of SITHCon to a Temporal Convolution Network (TCN) and demonstrate that, although both networks can learn classification and regression problems on both univariate and multivariate time series $f(t)$, only SITHCon has the property that it generalizes without retraining to rescaled versions of the input $f(at)$. This property, inspired by findings from neuroscience and psychology, could lead to large-scale networks with dramatically different capabilities, including faster training and greater generalizability, even with significantly fewer free parameters.