"What" x "When" working memory representations using Laplace Neural Manifolds

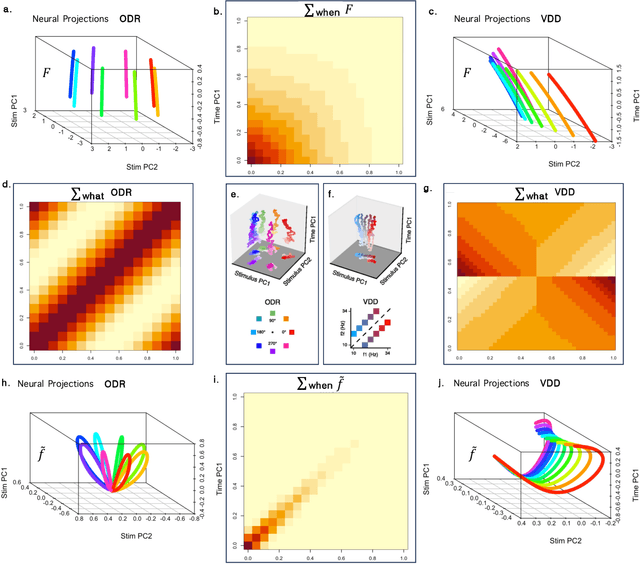
Working memory $\unicode{x2013}$ the ability to remember recent events as they recede continuously into the past $\unicode{x2013}$ requires the ability to represent any stimulus at any time delay. This property requires neurons coding working memory to show mixed selectivity, with conjunctive receptive fields (RFs) for stimuli and time, forming a representation of 'what' $\times$ 'when'. We study the properties of such a working memory in simple experiments where a single stimulus must be remembered for a short time. The requirement of conjunctive receptive fields allows the covariance matrix of the network to decouple neatly, allowing an understanding of the low-dimensional dynamics of the population. Different choices of temporal basis functions lead to qualitatively different dynamics. We study a specific choice $\unicode{x2013}$ a Laplace space with exponential basis functions for time coupled to an "Inverse Laplace" space with circumscribed basis functions in time. We refer to this choice with basis functions that evenly tile log time as a Laplace Neural Manifold. Despite the fact that they are related to one another by a linear projection, the Laplace population shows a stable stimulus-specific subspace whereas the Inverse Laplace population shows rotational dynamics. The growth of the rank of the covariance matrix with time depends on the density of the temporal basis set; logarithmic tiling shows good agreement with data. We sketch a continuous attractor CANN that constructs a Laplace Neural Manifold. The attractor in the Laplace space appears as an edge; the attractor for the inverse space appears as a bump. This work provides a map for going from more abstract cognitive models of WM to circuit-level implementation using continuous attractor neural networks, and places constraints on the types of neural dynamics that support working memory.

SITHCon: A neural network robust to variations in input scaling on the time dimension

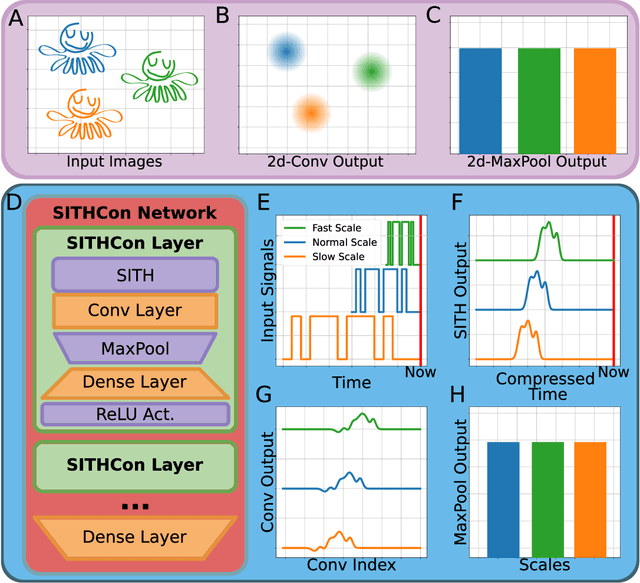
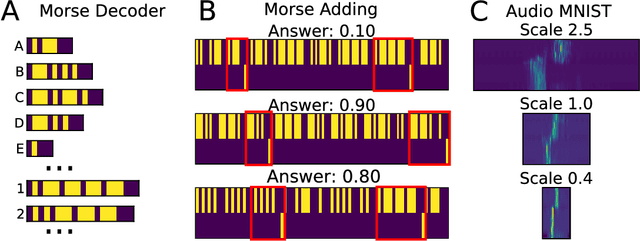
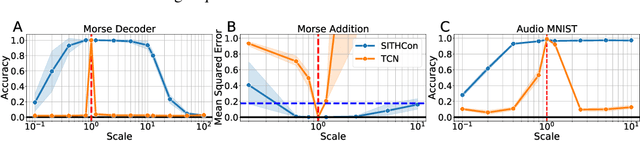
In machine learning, convolutional neural networks (CNNs) have been extremely influential in both computer vision and in recognizing patterns extended over time. In computer vision, part of the flexibility arises from the use of max-pooling operations over the convolutions to attain translation invariance. In the mammalian brain, neural representations of time use a set of temporal basis functions. Critically, these basis functions appear to be arranged in a geometric series such that the basis set is evenly distributed over logarithmic time. This paper introduces a Scale-Invariant Temporal History Convolution network (SITHCon) that uses a logarithmically-distributed temporal memory. A max-pool over a logarithmically-distributed temporal memory results in scale-invariance in time. We compare performance of SITHCon to a Temporal Convolution Network (TCN) and demonstrate that, although both networks can learn classification and regression problems on both univariate and multivariate time series $f(t)$, only SITHCon has the property that it generalizes without retraining to rescaled versions of the input $f(at)$. This property, inspired by findings from neuroscience and psychology, could lead to large-scale networks with dramatically different capabilities, including faster training and greater generalizability, even with significantly fewer free parameters.

Scale-dependent Relationships in Natural Language

Natural language exhibits statistical dependencies at a wide range of scales. For instance, the mutual information between words in natural language decays like a power law with the temporal lag between them. However, many statistical learning models applied to language impose a sampling scale while extracting statistical structure. For instance, Word2Vec constructs a vector embedding that maximizes the prediction between a target word and the context words that appear nearby in the corpus. The size of the context is chosen by the user and defines a strong scale; relationships over much larger temporal scales would be invisible to the algorithm. This paper examines the family of Word2Vec embeddings generated while systematically manipulating the sampling scale used to define the context around each word. The primary result is that different linguistic relationships are preferentially encoded at different scales. Different scales emphasize different syntactic and semantic relations between words.Moreover, the neighborhoods of a given word in the embeddings change significantly depending on the scale. These results suggest that any individual scale can only identify a subset of the meaningful relationships a word might have, and point toward the importance of developing scale-free models of semantic meaning.