Shangfu Zuo
"What" x "When" working memory representations using Laplace Neural Manifolds
Sep 30, 2024

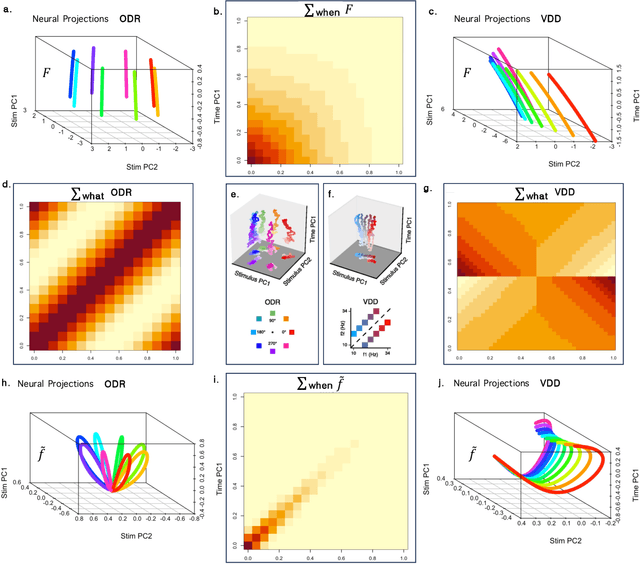

Abstract:Working memory $\unicode{x2013}$ the ability to remember recent events as they recede continuously into the past $\unicode{x2013}$ requires the ability to represent any stimulus at any time delay. This property requires neurons coding working memory to show mixed selectivity, with conjunctive receptive fields (RFs) for stimuli and time, forming a representation of 'what' $\times$ 'when'. We study the properties of such a working memory in simple experiments where a single stimulus must be remembered for a short time. The requirement of conjunctive receptive fields allows the covariance matrix of the network to decouple neatly, allowing an understanding of the low-dimensional dynamics of the population. Different choices of temporal basis functions lead to qualitatively different dynamics. We study a specific choice $\unicode{x2013}$ a Laplace space with exponential basis functions for time coupled to an "Inverse Laplace" space with circumscribed basis functions in time. We refer to this choice with basis functions that evenly tile log time as a Laplace Neural Manifold. Despite the fact that they are related to one another by a linear projection, the Laplace population shows a stable stimulus-specific subspace whereas the Inverse Laplace population shows rotational dynamics. The growth of the rank of the covariance matrix with time depends on the density of the temporal basis set; logarithmic tiling shows good agreement with data. We sketch a continuous attractor CANN that constructs a Laplace Neural Manifold. The attractor in the Laplace space appears as an edge; the attractor for the inverse space appears as a bump. This work provides a map for going from more abstract cognitive models of WM to circuit-level implementation using continuous attractor neural networks, and places constraints on the types of neural dynamics that support working memory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge