High Volatility and Action Bias Distinguish LLMs from Humans in Group Coordination

Humans exhibit remarkable abilities to coordinate in groups. As large language models (LLMs) become more capable, it remains an open question whether they can demonstrate comparable adaptive coordination and whether they use the same strategies as humans. To investigate this, we compare LLM and human performance on a common-interest game with imperfect monitoring: Group Binary Search. In this n-player game, participants need to coordinate their actions to achieve a common objective. Players independently submit numerical values in an effort to collectively sum to a randomly assigned target number. Without direct communication, they rely on group feedback to iteratively adjust their submissions until they reach the target number. Our findings show that, unlike humans who adapt and stabilize their behavior over time, LLMs often fail to improve across games and exhibit excessive switching, which impairs group convergence. Moreover, richer feedback (e.g., numerical error magnitude) benefits humans substantially but has small effects on LLMs. Taken together, by grounding the analysis in human baselines and mechanism-level metrics, including reactivity scaling, switching dynamics, and learning across games, we point to differences in human and LLM groups and provide a behaviorally grounded diagnostic for closing the coordination gap.

Temporal Dependencies in In-Context Learning: The Role of Induction Heads

Large language models (LLMs) exhibit strong in-context learning capabilities, but how they track and retrieve information from context remains underexplored. Drawing on the free recall paradigm in cognitive science (where participants recall list items in any order), we show that several open-source LLMs consistently display a serial-recall-like pattern, assigning peak probability to tokens that immediately follow a repeated token in the input sequence. Through systematic ablation experiments, we show that induction heads, specialized attention heads that attend to the token following a previous occurrence of the current token, play an important role in this phenomenon. Removing heads with a high induction score substantially reduces the +1 lag bias, whereas ablating random heads does not reproduce the same reduction. We also show that removing heads with high induction scores impairs the performance of models prompted to do serial recall using few-shot learning to a larger extent than removing random heads. Our findings highlight a mechanistically specific connection between induction heads and temporal context processing in transformers, suggesting that these heads are especially important for ordered retrieval and serial-recall-like behavior during in-context learning.

Who Do LLMs Trust? Human Experts Matter More Than Other LLMs

Large language models (LLMs) increasingly operate in environments where they encounter social information such as other agents' answers, tool outputs, or human recommendations. In humans, such inputs influence judgments in ways that depend on the source's credibility and the strength of consensus. This paper investigates whether LLMs exhibit analogous patterns of influence and whether they privilege feedback from humans over feedback from other LLMs. Across three binary decision-making tasks, reading comprehension, multi-step reasoning, and moral judgment, we present four instruction-tuned LLMs with prior responses attributed either to friends, to human experts, or to other LLMs. We manipulate whether the group is correct and vary the group size. In a second experiment, we introduce direct disagreement between a single human and a single LLM. Across tasks, models conform significantly more to responses labeled as coming from human experts, including when that signal is incorrect, and revise their answers toward experts more readily than toward other LLMs. These results reveal that expert framing acts as a strong prior for contemporary LLMs, suggesting a form of credibility-sensitive social influence that generalizes across decision domains.

Beyond Semantics: How Temporal Biases Shape Retrieval in Transformer and State-Space Models

In-context learning is governed by both temporal and semantic relationships, shaping how Large Language Models (LLMs) retrieve contextual information. Analogous to human episodic memory, where the retrieval of specific events is enabled by separating events that happened at different times, this work probes the ability of various pretrained LLMs, including transformer and state-space models, to differentiate and retrieve temporally separated events. Specifically, we prompted models with sequences containing multiple presentations of the same token, which reappears at the sequence end. By fixing the positions of these repeated tokens and permuting all others, we removed semantic confounds and isolated temporal effects on next-token prediction. Across diverse sequences, models consistently placed the highest probabilities on tokens following a repeated token, but with a notable bias for those nearest the beginning or end of the input. An ablation experiment linked this phenomenon in transformers to induction heads. Extending the analysis to unique semantic contexts with partial overlap further demonstrated that memories embedded in the middle of a prompt are retrieved less reliably. Despite architectural differences, state-space and transformer models showed comparable temporal biases. Our findings deepen the understanding of temporal biases in in-context learning and offer an illustration of how these biases can enable temporal separation and episodic retrieval.

Emergence of Episodic Memory in Transformers: Characterizing Changes in Temporal Structure of Attention Scores During Training

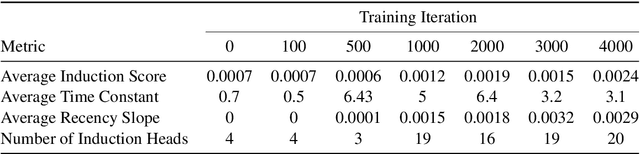
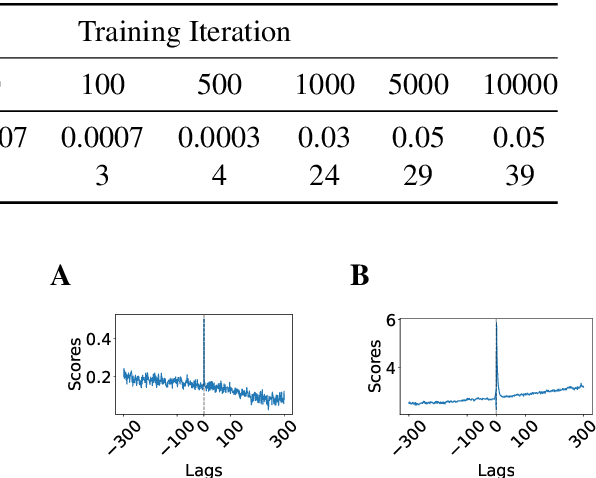
We investigate in-context temporal biases in attention heads and transformer outputs. Using cognitive science methodologies, we analyze attention scores and outputs of the GPT-2 models of varying sizes. Across attention heads, we observe effects characteristic of human episodic memory, including temporal contiguity, primacy and recency. Transformer outputs demonstrate a tendency toward in-context serial recall. Importantly, this effect is eliminated after the ablation of the induction heads, which are the driving force behind the contiguity effect. Our findings offer insights into how transformers organize information temporally during in-context learning, shedding light on their similarities and differences with human memory and learning.

Deep reinforcement learning with time-scale invariant memory

The ability to estimate temporal relationships is critical for both animals and artificial agents. Cognitive science and neuroscience provide remarkable insights into behavioral and neural aspects of temporal credit assignment. In particular, scale invariance of learning dynamics, observed in behavior and supported by neural data, is one of the key principles that governs animal perception: proportional rescaling of temporal relationships does not alter the overall learning efficiency. Here we integrate a computational neuroscience model of scale invariant memory into deep reinforcement learning (RL) agents. We first provide a theoretical analysis and then demonstrate through experiments that such agents can learn robustly across a wide range of temporal scales, unlike agents built with commonly used recurrent memory architectures such as LSTM. This result illustrates that incorporating computational principles from neuroscience and cognitive science into deep neural networks can enhance adaptability to complex temporal dynamics, mirroring some of the core properties of human learning.

SITHCon: A neural network robust to variations in input scaling on the time dimension

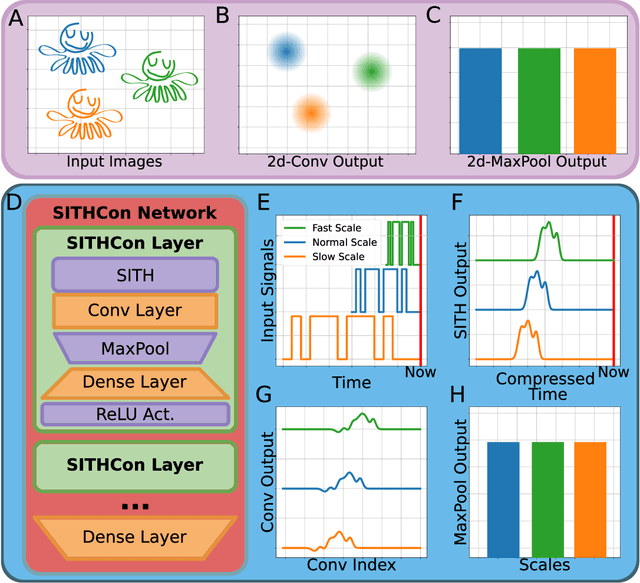
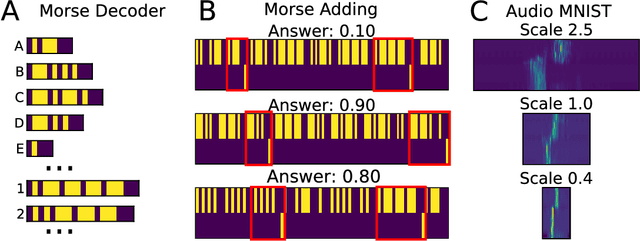
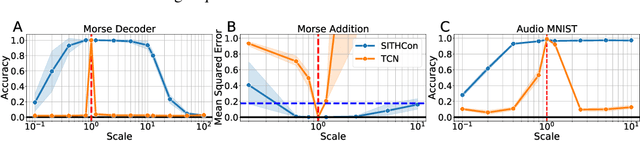
In machine learning, convolutional neural networks (CNNs) have been extremely influential in both computer vision and in recognizing patterns extended over time. In computer vision, part of the flexibility arises from the use of max-pooling operations over the convolutions to attain translation invariance. In the mammalian brain, neural representations of time use a set of temporal basis functions. Critically, these basis functions appear to be arranged in a geometric series such that the basis set is evenly distributed over logarithmic time. This paper introduces a Scale-Invariant Temporal History Convolution network (SITHCon) that uses a logarithmically-distributed temporal memory. A max-pool over a logarithmically-distributed temporal memory results in scale-invariance in time. We compare performance of SITHCon to a Temporal Convolution Network (TCN) and demonstrate that, although both networks can learn classification and regression problems on both univariate and multivariate time series $f(t)$, only SITHCon has the property that it generalizes without retraining to rescaled versions of the input $f(at)$. This property, inspired by findings from neuroscience and psychology, could lead to large-scale networks with dramatically different capabilities, including faster training and greater generalizability, even with significantly fewer free parameters.

DeepSITH: Efficient Learning via Decomposition of What and When Across Time Scales

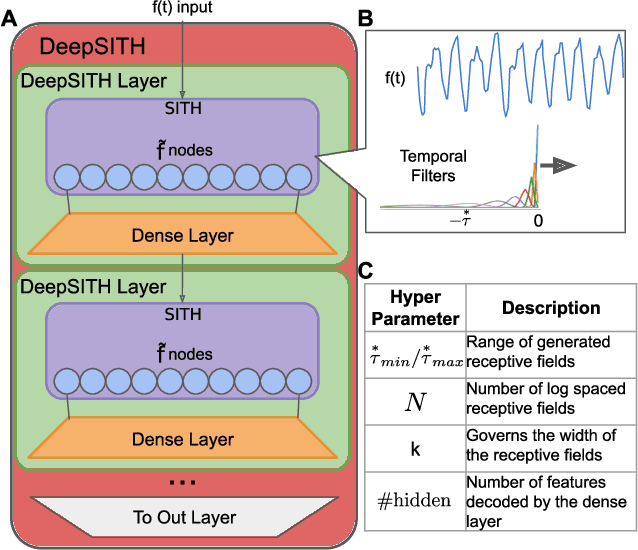
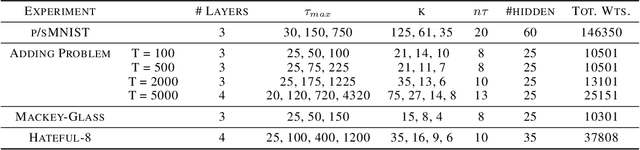
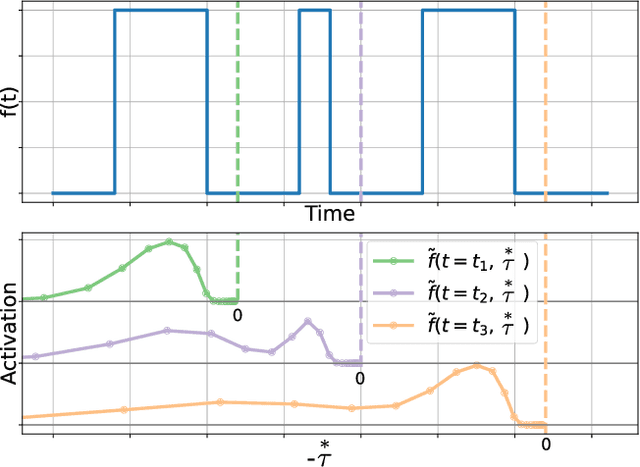
Extracting temporal relationships over a range of scales is a hallmark of human perception and cognition -- and thus it is a critical feature of machine learning applied to real-world problems. Neural networks are either plagued by the exploding/vanishing gradient problem in recurrent neural networks (RNNs) or must adjust their parameters to learn the relevant time scales (e.g., in LSTMs). This paper introduces DeepSITH, a network comprising biologically-inspired Scale-Invariant Temporal History (SITH) modules in series with dense connections between layers. SITH modules respond to their inputs with a geometrically-spaced set of time constants, enabling the DeepSITH network to learn problems along a continuum of time-scales. We compare DeepSITH to LSTMs and other recent RNNs on several time series prediction and decoding tasks. DeepSITH achieves state-of-the-art performance on these problems.

Estimating scale-invariant future in continuous time

Natural learners must compute an estimate of future outcomes that follow from a stimulus in continuous time. Widely used reinforcement learning algorithms discretize continuous time and estimate either transition functions from one step to the next (model-based algorithms) or a scalar value of exponentially-discounted future reward using the Bellman equation (model-free algorithms). An important drawback of model-based algorithms is that computational cost grows linearly with the amount of time to be simulated. On the other hand, an important drawback of model-free algorithms is the need to select a time-scale required for exponential discounting. We present a computational mechanism, developed based on work in psychology and neuroscience, for computing a scale-invariant timeline of future outcomes. This mechanism efficiently computes an estimate of inputs as a function of future time on a logarithmically-compressed scale, and can be used to generate a scale-invariant power-law-discounted estimate of expected future reward. The representation of future time retains information about what will happen when. The entire timeline can be constructed in a single parallel operation which generates concrete behavioral and neural predictions. This computational mechanism could be incorporated into future reinforcement learning algorithms.