Generic construction of scale-invariantly coarse grained memory

Encoding temporal information from the recent past as spatially distributed activations is essential in order for the entire recent past to be simultaneously accessible. Any biological or synthetic agent that relies on the past to predict/plan the future, would be endowed with such a spatially distributed temporal memory. Simplistically, we would expect that resource limitations would demand the memory system to store only the most useful information for future prediction. For natural signals in real world which show scale free temporal fluctuations, the predictive information encoded in memory is maximal if the past information is scale invariantly coarse grained. Here we examine the general mechanism to construct a scale invariantly coarse grained memory system. Remarkably, the generic construction is equivalent to encoding the linear combinations of Laplace transform of the past information and their approximated inverses. This reveals a fundamental construction constraint on memory networks that attempt to maximize predictive information storage relevant to the natural world.

Optimally fuzzy temporal memory

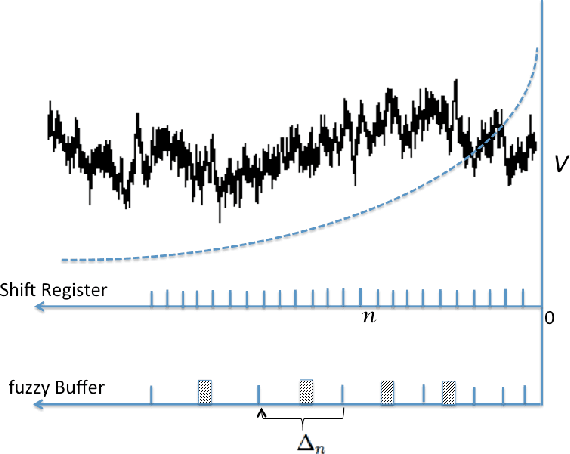
Any learner with the ability to predict the future of a structured time-varying signal must maintain a memory of the recent past. If the signal has a characteristic timescale relevant to future prediction, the memory can be a simple shift register---a moving window extending into the past, requiring storage resources that linearly grows with the timescale to be represented. However, an independent general purpose learner cannot a priori know the characteristic prediction-relevant timescale of the signal. Moreover, many naturally occurring signals show scale-free long range correlations implying that the natural prediction-relevant timescale is essentially unbounded. Hence the learner should maintain information from the longest possible timescale allowed by resource availability. Here we construct a fuzzy memory system that optimally sacrifices the temporal accuracy of information in a scale-free fashion in order to represent prediction-relevant information from exponentially long timescales. Using several illustrative examples, we demonstrate the advantage of the fuzzy memory system over a shift register in time series forecasting of natural signals. When the available storage resources are limited, we suggest that a general purpose learner would be better off committing to such a fuzzy memory system.