The Resume Paradox: Greater Language Differences, Smaller Pay Gaps

Over the past decade, the gender pay gap has remained steady with women earning 84 cents for every dollar earned by men on average. Many studies explain this gap through demand-side bias in the labor market represented through employers' job postings. However, few studies analyze potential bias from the worker supply-side. Here, we analyze the language in millions of US workers' resumes to investigate how differences in workers' self-representation by gender compare to differences in earnings. Across US occupations, language differences between male and female resumes correspond to 11% of the variation in gender pay gap. This suggests that females' resumes that are semantically similar to males' resumes may have greater wage parity. However, surprisingly, occupations with greater language differences between male and female resumes have lower gender pay gaps. A doubling of the language difference between female and male resumes results in an annual wage increase of $2,797 for the average female worker. This result holds with controls for gender-biases of resume text and we find that per-word bias poorly describes the variance in wage gap. The results demonstrate that textual data and self-representation are valuable factors for improving worker representations and understanding employment inequities.

Interpretable bias mitigation for textual data: Reducing gender bias in patient notes while maintaining classification performance

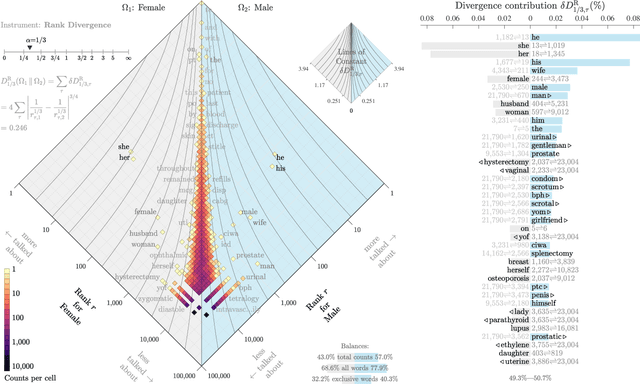
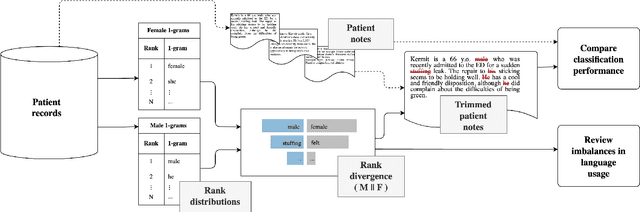
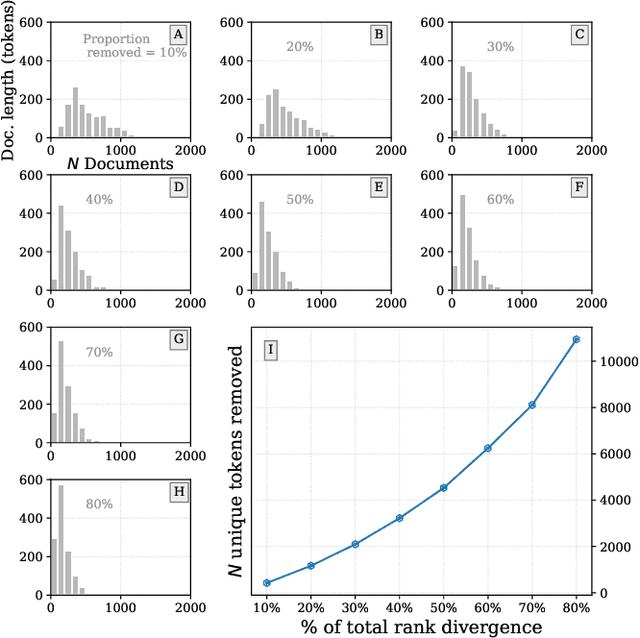
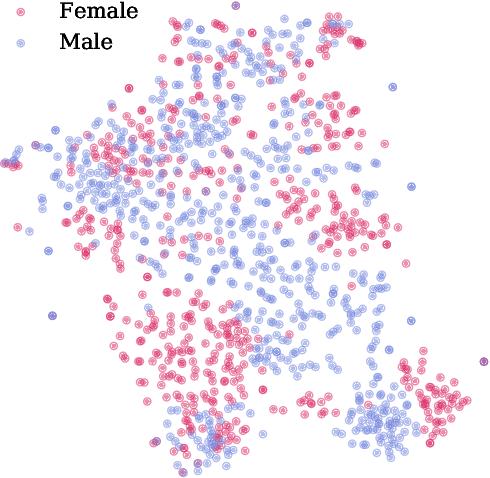
Medical systems in general, and patient treatment decisions and outcomes in particular, are affected by bias based on gender and other demographic elements. As language models are increasingly applied to medicine, there is a growing interest in building algorithmic fairness into processes impacting patient care. Much of the work addressing this question has focused on biases encoded in language models -- statistical estimates of the relationships between concepts derived from distant reading of corpora. Building on this work, we investigate how word choices made by healthcare practitioners and language models interact with regards to bias. We identify and remove gendered language from two clinical-note datasets and describe a new debiasing procedure using BERT-based gender classifiers. We show minimal degradation in health condition classification tasks for low- to medium-levels of bias removal via data augmentation. Finally, we compare the bias semantically encoded in the language models with the bias empirically observed in health records. This work outlines an interpretable approach for using data augmentation to identify and reduce the potential for bias in natural language processing pipelines.

Reasoning about Independence in Probabilistic Models of Relational Data

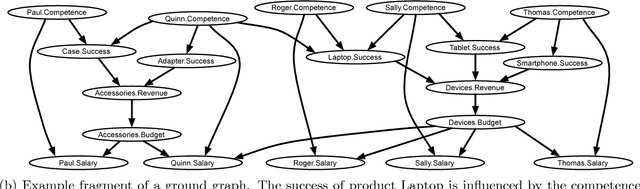
We extend the theory of d-separation to cases in which data instances are not independent and identically distributed. We show that applying the rules of d-separation directly to the structure of probabilistic models of relational data inaccurately infers conditional independence. We introduce relational d-separation, a theory for deriving conditional independence facts from relational models. We provide a new representation, the abstract ground graph, that enables a sound, complete, and computationally efficient method for answering d-separation queries about relational models, and we present empirical results that demonstrate effectiveness.

A Sound and Complete Algorithm for Learning Causal Models from Relational Data

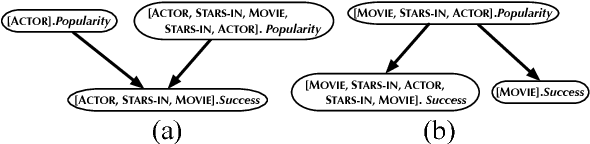
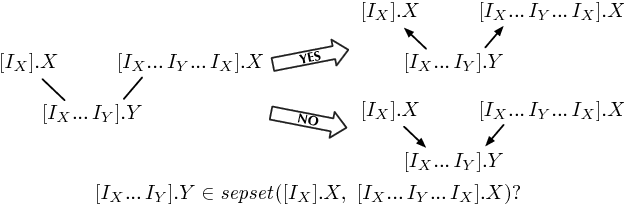
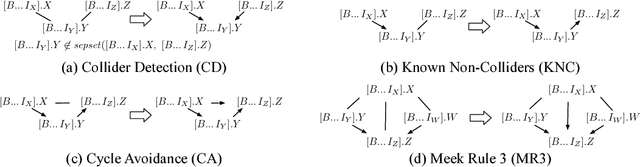
The PC algorithm learns maximally oriented causal Bayesian networks. However, there is no equivalent complete algorithm for learning the structure of relational models, a more expressive generalization of Bayesian networks. Recent developments in the theory and representation of relational models support lifted reasoning about conditional independence. This enables a powerful constraint for orienting bivariate dependencies and forms the basis of a new algorithm for learning structure. We present the relational causal discovery (RCD) algorithm that learns causal relational models. We prove that RCD is sound and complete, and we present empirical results that demonstrate effectiveness.

Identifying Independence in Relational Models

The rules of d-separation provide a framework for deriving conditional independence facts from model structure. However, this theory only applies to simple directed graphical models. We introduce relational d-separation, a theory for deriving conditional independence in relational models. We provide a sound, complete, and computationally efficient method for relational d-separation, and we present empirical results that demonstrate effectiveness.