Any-Width Networks

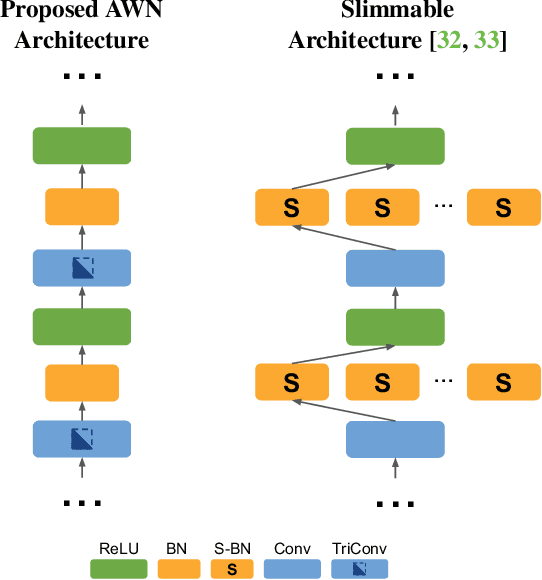
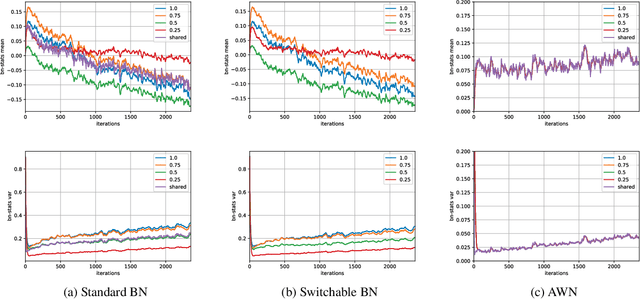
Despite remarkable improvements in speed and accuracy, convolutional neural networks (CNNs) still typically operate as monolithic entities at inference time. This poses a challenge for resource-constrained practical applications, where both computational budgets and performance needs can vary with the situation. To address these constraints, we propose the Any-Width Network (AWN), an adjustable-width CNN architecture and associated training routine that allow for fine-grained control over speed and accuracy during inference. Our key innovation is the use of lower-triangular weight matrices which explicitly address width-varying batch statistics while being naturally suited for multi-width operations. We also show that this design facilitates an efficient training routine based on random width sampling. We empirically demonstrate that our proposed AWNs compare favorably to existing methods while providing maximally granular control during inference.

Tangent Images for Mitigating Spherical Distortion

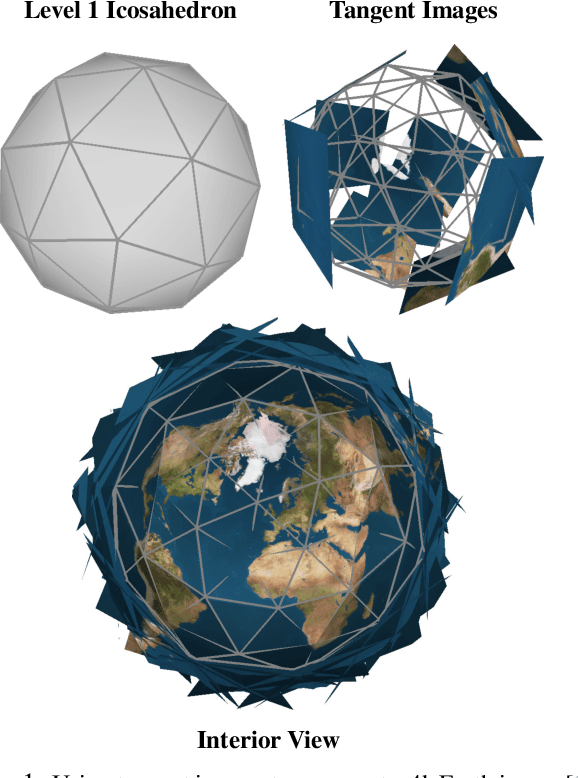
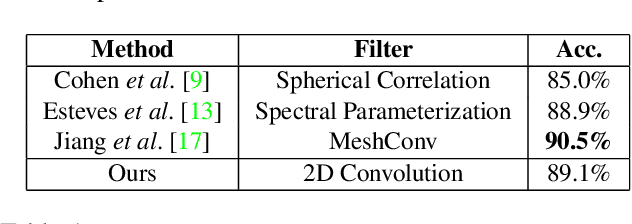
In this work, we propose "tangent images," a spherical image representation that facilitates transferable and scalable $360^\circ$ computer vision. Inspired by techniques in cartography and computer graphics, we render a spherical image to a set of distortion-mitigated, locally-planar image grids tangent to a subdivided icosahedron. By varying the resolution of these grids independently of the subdivision level, we can effectively represent high resolution spherical images while still benefiting from the low-distortion icosahedral spherical approximation. We show that training standard convolutional neural networks on tangent images compares favorably to the many specialized spherical convolutional kernels that have been developed, while also allowing us to scale training to significantly higher spherical resolutions. Furthermore, because we do not require specialized kernels, we show that we can transfer networks trained on perspective images to spherical data without fine-tuning and with limited performance drop-off. Finally, we demonstrate that tangent images can be used to improve the quality of sparse feature detection on spherical images, illustrating its usefulness for traditional computer vision tasks like structure-from-motion and SLAM.

Pano Popups: Indoor 3D Reconstruction with a Plane-Aware Network

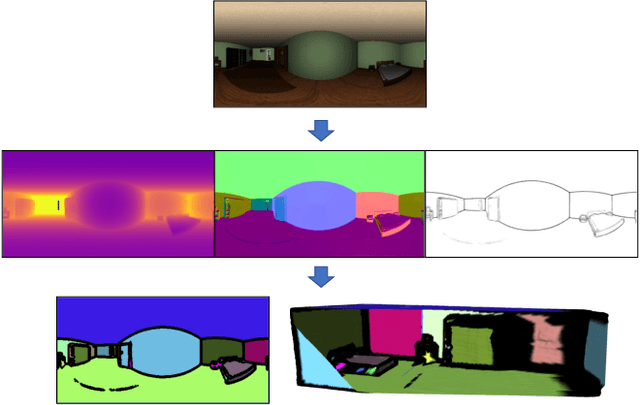
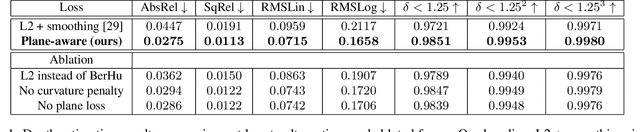
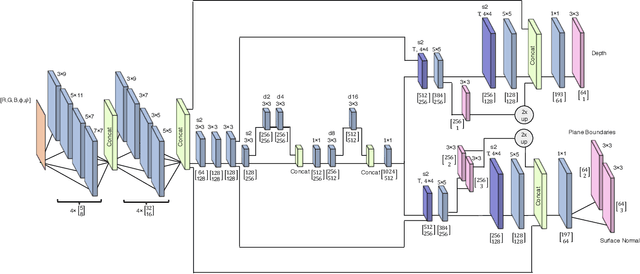
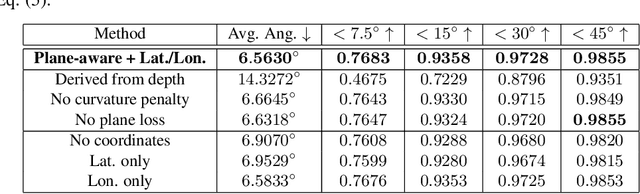
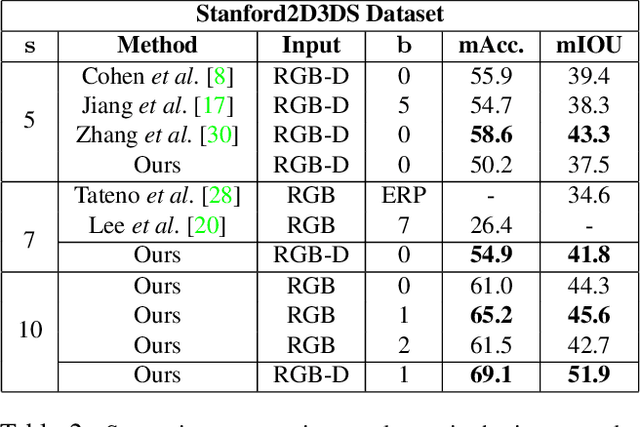
In this work we present a method to train a plane-aware convolutional neural network for dense depth and surface normal estimation as well as plane boundaries from a single indoor \threesixty image. Using our proposed loss function, our network outperforms existing methods for single-view, indoor, omnidirectional depth estimation and provides an initial benchmark for surface normal prediction from \threesixty images. Our improvements are due to the use of a novel plane-aware loss that leverages principal curvature as an indicator of planar boundaries. We also show that including geodesic coordinate maps as network priors provides a significant boost in surface normal prediction accuracy. Finally, we demonstrate how we can combine our network's outputs to generate high quality 3D ``pop-up" models of indoor scenes.

Mapped Convolutions

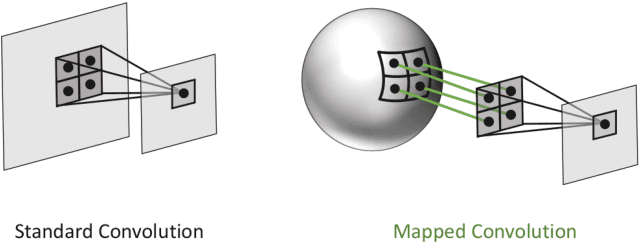
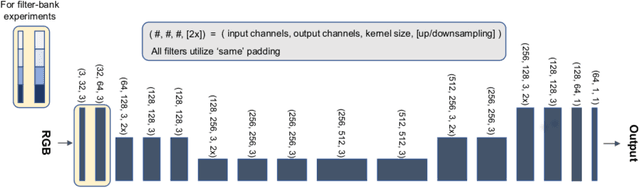
We present a versatile formulation of the convolution operation that we term a "mapped convolution." The standard convolution operation implicitly samples the pixel grid and computes a weighted sum. Our mapped convolution decouples these two components, freeing the operation from the confines of the image grid and allowing the kernel to process any type of structured data. As a test case, we demonstrate its use by applying it to dense inference on spherical data. We perform an in-depth study of existing spherical image convolution methods and propose an improved sampling method for equirectangular images. Then, we discuss the impact of data discretization when deriving a sampling function, highlighting drawbacks of the cube map representation for spherical data. Finally, we illustrate how mapped convolutions enable us to convolve directly on a mesh by projecting the spherical image onto a geodesic grid and training on the textured mesh. This method exceeds the state of the art for spherical depth estimation by nearly 17%. Our findings suggest that mapped convolutions can be instrumental in expanding the application scope of convolutional neural networks.

Convolutions on Spherical Images

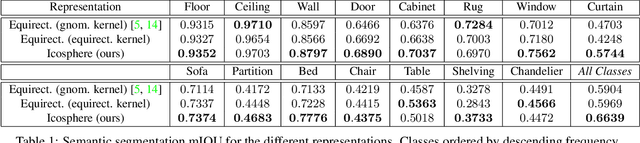
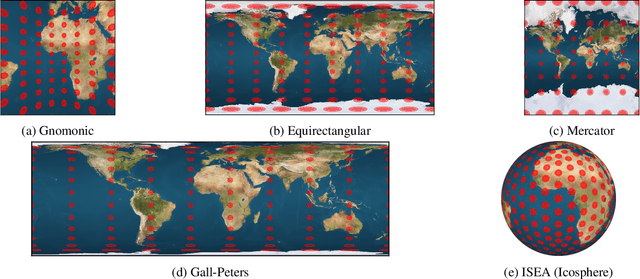
Applying convolutional neural networks to spherical images requires particular considerations. We look to the millennia of work on cartographic map projections to provide the tools to define an optimal representation of spherical images for the convolution operation. We propose a representation for deep spherical image inference based on the icosahedral Snyder equal-area (ISEA) projection, a projection onto a geodesic grid, and show that it vastly exceeds the state-of-the-art for convolution on spherical images, improving semantic segmentation results by 12.6%.