Mapped Convolutions
Paper and Code
Jun 26, 2019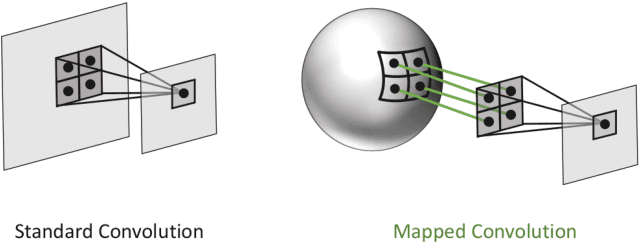


We present a versatile formulation of the convolution operation that we term a "mapped convolution." The standard convolution operation implicitly samples the pixel grid and computes a weighted sum. Our mapped convolution decouples these two components, freeing the operation from the confines of the image grid and allowing the kernel to process any type of structured data. As a test case, we demonstrate its use by applying it to dense inference on spherical data. We perform an in-depth study of existing spherical image convolution methods and propose an improved sampling method for equirectangular images. Then, we discuss the impact of data discretization when deriving a sampling function, highlighting drawbacks of the cube map representation for spherical data. Finally, we illustrate how mapped convolutions enable us to convolve directly on a mesh by projecting the spherical image onto a geodesic grid and training on the textured mesh. This method exceeds the state of the art for spherical depth estimation by nearly 17%. Our findings suggest that mapped convolutions can be instrumental in expanding the application scope of convolutional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge