FedOSAA: Improving Federated Learning with One-Step Anderson Acceleration

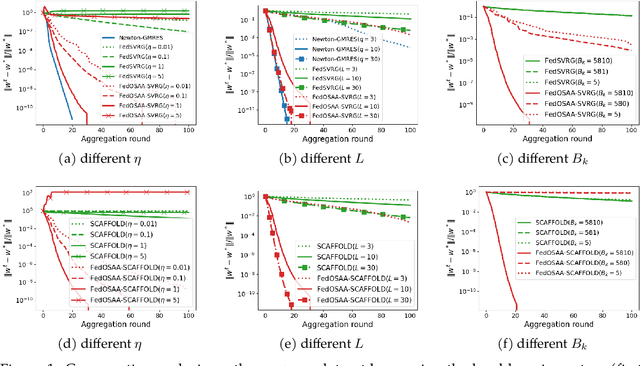
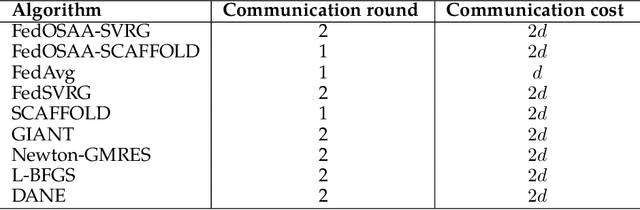
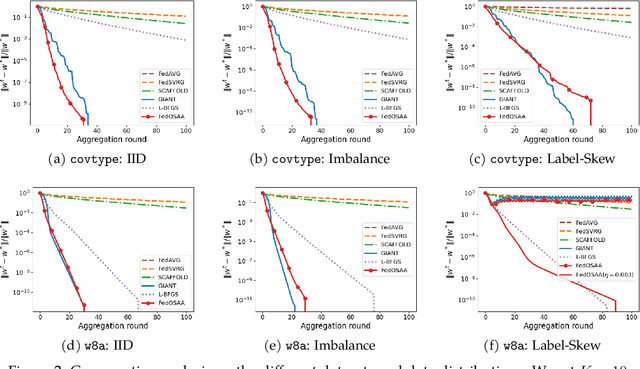
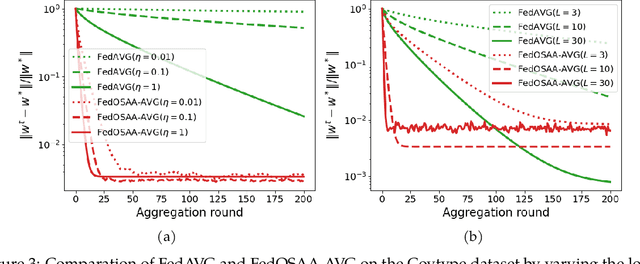
Federated learning (FL) is a distributed machine learning approach that enables multiple local clients and a central server to collaboratively train a model while keeping the data on their own devices. First-order methods, particularly those incorporating variance reduction techniques, are the most widely used FL algorithms due to their simple implementation and stable performance. However, these methods tend to be slow and require a large number of communication rounds to reach the global minimizer. We propose FedOSAA, a novel approach that preserves the simplicity of first-order methods while achieving the rapid convergence typically associated with second-order methods. Our approach applies one Anderson acceleration (AA) step following classical local updates based on first-order methods with variance reduction, such as FedSVRG and SCAFFOLD, during local training. This AA step is able to leverage curvature information from the history points and gives a new update that approximates the Newton-GMRES direction, thereby significantly improving the convergence. We establish a local linear convergence rate to the global minimizer of FedOSAA for smooth and strongly convex loss functions. Numerical comparisons show that FedOSAA substantially improves the communication and computation efficiency of the original first-order methods, achieving performance comparable to second-order methods like GIANT.

MATEY: multiscale adaptive foundation models for spatiotemporal physical systems

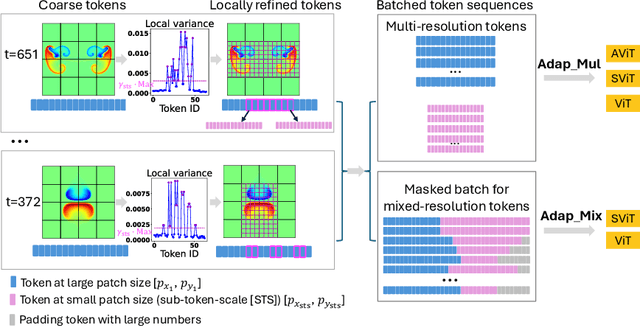
Accurate representation of the multiscale features in spatiotemporal physical systems using vision transformer (ViT) architectures requires extremely long, computationally prohibitive token sequences. To address this issue, we propose two adaptive tokenization schemes that dynamically adjust patch sizes based on local features: one ensures convergent behavior to uniform patch refinement, while the other offers better computational efficiency. Moreover, we present a set of spatiotemporal attention schemes, where the temporal or axial spatial dimensions are decoupled, and evaluate their computational and data efficiencies. We assess the performance of the proposed multiscale adaptive model, MATEY, in a sequence of experiments. The results show that adaptive tokenization schemes achieve improved accuracy without significantly increasing the length of the token sequence. Compared to a full spatiotemporal attention scheme or a scheme that decouples only the temporal dimension, we find that fully decoupled axial attention is less efficient and expressive, requiring more training time and model weights to achieve the same accuracy. Finally, we demonstrate in two fine-tuning tasks featuring different physics that models pretrained on PDEBench data outperform the ones trained from scratch, especially in the low data regime with frozen attention.

Federated Dynamical Low-Rank Training with Global Loss Convergence Guarantees

In this work, we propose a federated dynamical low-rank training (FeDLRT) scheme to reduce client compute and communication costs - two significant performance bottlenecks in horizontal federated learning. Our method builds upon dynamical low-rank splitting schemes for manifold-constrained optimization to create a global low-rank basis of network weights, which enables client training on a small coefficient matrix. A consistent global low-rank basis allows us to incorporate a variance correction scheme and prove global loss descent and convergence to a stationary point. Dynamic augmentation and truncation of the low-rank bases automatically optimizes computing and communication resource utilization. We demonstrate the efficiency of FeDLRT in an array of computer vision benchmarks and show a reduction of client compute and communication costs by up to an order of magnitude with minimal impacts on global accuracy.

Structure-preserving neural networks for the regularized entropy-based closure of the Boltzmann moment system

The main challenge of large-scale numerical simulation of radiation transport is the high memory and computation time requirements of discretization methods for kinetic equations. In this work, we derive and investigate a neural network-based approximation to the entropy closure method to accurately compute the solution of the multi-dimensional moment system with a low memory footprint and competitive computational time. We extend methods developed for the standard entropy-based closure to the context of regularized entropy-based closures. The main idea is to interpret structure-preserving neural network approximations of the regularized entropy closure as a two-stage approximation to the original entropy closure. We conduct a numerical analysis of this approximation and investigate optimal parameter choices. Our numerical experiments demonstrate that the method has a much lower memory footprint than traditional methods with competitive computation times and simulation accuracy. The code and all trained networks are provided on GitHub https://github.com/ScSteffen/neuralEntropyClosures and https://github.com/CSMMLab/KiT-RT.

Streaming Compression of Scientific Data via weak-SINDy

In this paper a streaming weak-SINDy algorithm is developed specifically for compressing streaming scientific data. The production of scientific data, either via simulation or experiments, is undergoing an stage of exponential growth, which makes data compression important and often necessary for storing and utilizing large scientific data sets. As opposed to classical ``offline" compression algorithms that perform compression on a readily available data set, streaming compression algorithms compress data ``online" while the data generated from simulation or experiments is still flowing through the system. This feature makes streaming compression algorithms well-suited for scientific data compression, where storing the full data set offline is often infeasible. This work proposes a new streaming compression algorithm, streaming weak-SINDy, which takes advantage of the underlying data characteristics during compression. The streaming weak-SINDy algorithm constructs feature matrices and target vectors in the online stage via a streaming integration method in a memory efficient manner. The feature matrices and target vectors are then used in the offline stage to build a model through a regression process that aims to recover equations that govern the evolution of the data. For compressing high-dimensional streaming data, we adopt a streaming proper orthogonal decomposition (POD) process to reduce the data dimension and then use the streaming weak-SINDy algorithm to compress the temporal data of the POD expansion. We propose modifications to the streaming weak-SINDy algorithm to accommodate the dynamically updated POD basis. By combining the built model from the streaming weak-SINDy algorithm and a small amount of data samples, the full data flow could be reconstructed accurately at a low memory cost, as shown in the numerical tests.

Convergence of weak-SINDy Surrogate Models

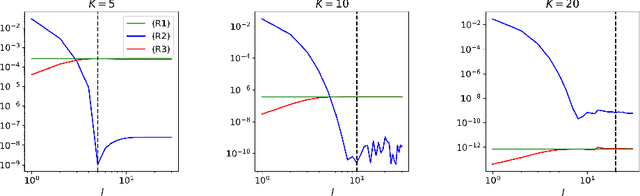
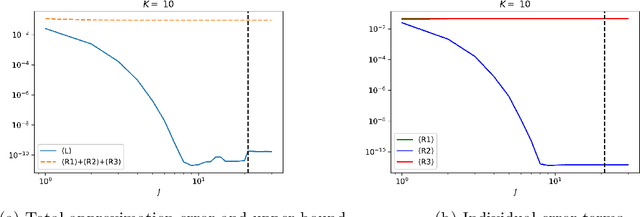
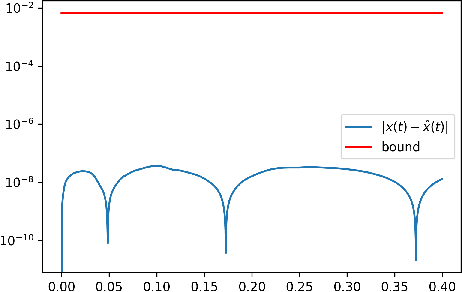
In this paper, we give an in-depth error analysis for surrogate models generated by a variant of the Sparse Identification of Nonlinear Dynamics (SINDy) method. We start with an overview of a variety of non-linear system identification techniques, namely, SINDy, weak-SINDy, and the occupation kernel method. Under the assumption that the dynamics are a finite linear combination of a set of basis functions, these methods establish a matrix equation to recover coefficients. We illuminate the structural similarities between these techniques and establish a projection property for the weak-SINDy technique. Following the overview, we analyze the error of surrogate models generated by a simplified version of weak-SINDy. In particular, under the assumption of boundedness of a composition operator given by the solution, we show that (i) the surrogate dynamics converges towards the true dynamics and (ii) the solution of the surrogate model is reasonably close to the true solution. Finally, as an application, we discuss the use of a combination of weak-SINDy surrogate modeling and proper orthogonal decomposition (POD) to build a surrogate model for partial differential equations (PDEs).